Advertisements
Advertisements
प्रश्न
In the given figure, the area of the shaded portion is 770 cm2. If the circumference of the outer circle is 132 cm, find the width of the shaded portion.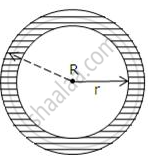
उत्तर
From the given data, we can calculate the area of the outer circle and then the area of the inner circle and hence the width of the shaded portion.
Given that the circumference of the outer circle is 132 cm
Thus, we have, 2πR = 132 cm
⇒ R = `[ 132 xx 7 ]/[ 2 xx 22 ]`
⇒ R = 21 cm
Area of the bigger circle = πR2
= `22/7` × 212
= 1386 cm2
Also given the area of the shaded portion.
Thus, the area of the inner circle = Area of the outer circle - Area of the shaded portion
= 1386 - 770
= 616 cm2
⇒ πr2 = 616
⇒ r2 = `[ 616 xx 7 ]/22`
⇒ r2 = 196
⇒ r = 14 cm
Thus, the width of the shaded portion = 21 - 14 = 7 cm.
APPEARS IN
संबंधित प्रश्न
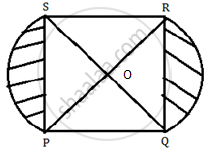
In the figure given below, PQRS is square lawn with side PQ = 42 metres. Two circular flower beds are there on the sides PS and QR with centre at O, the intersections of its
diagonals. Find the total area of the two flower beds (shaded parts).
The perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm. Find the area of the sector.
A horse is tied to a pole with 28m long string. Find the area where the horse can graze.
A road which is 7m wide surrounds a circular park whose circumference is 352m. Find the area of road.
The shape of the cross section of a canal is a trapezium. If the canal is 10 m wide at the top, 6 m wide at the bottom and the area of its cross section is `640m^2` , find the depth of the canal.
Find the diameter of the circle whose area is equal to the sum of the areas of two circles having radii 4 cm and 3 cm.
The circumference of a circle is 8 cm. Find the area of the sector whose central angle is 72°.
Find the curved surface area , the total surface area and the volume of a cone if its :
Height = 16 cm , diameter = 24 cm
Diameters of different circles are given below. Find their circumference (Take π = `22/7`)
d = 28 mm
In reference to a circle the value of π is equal to ______.
