Advertisements
Advertisements
प्रश्न
Find the curved surface area , the total surface area and the volume of a cone if its :
Height = 16 cm , diameter = 24 cm
उत्तर
Height = 16 cm , diameter = 24 cm
diameter = 24 cm ⇒ r = 12 cm
Curved surface area = `(pir sqrt(h^2 + r^2))`
= `22/7 xx 12 xx sqrt(16^2 + 12^2)`
= `22/7 xx 12 xx sqrt(400)`
= `22/7 xx 12 xx 20`
= 754.29
Curved surface area = 754.29 cm2
Total surface area = area of circular base + Curved surface area
= `pir^2 + (pir sqrt(h^2 + r^2))`
= `22/7 xx 12 xx 12 + 754.29`
= 452.57 + 754.29
= 1206 . 86
Total surface area = 1206.86 cm2
Volume = `1/3 xx (pir^2) xx h`
= `1/3 xx 22/7 xx 12 xx 12 xx 16`
= 2413.71
Volume of the cone = 2413.71 cm3
APPEARS IN
संबंधित प्रश्न
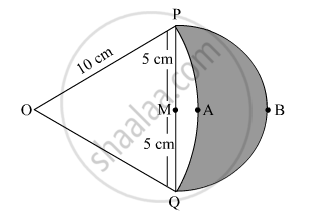
In Fig. 7, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre O and radius OP while arc PBQ is a semi-circle drawn on PQ ad diameter with centre M. If OP = PQ = 10 cm show that area of shaded region is `25(sqrt3-pi/6)cm^2`.
A bicycle whell makes 5000 revolutions in moving 11 km. Find the diameter of the wheel
Saima wants to put a lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one meter of the lace costs ₹ 15. (Take π = 3.14)
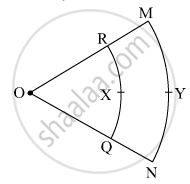
In the given figure, O is the centre of the sector. \[\angle\]ROQ = \[\angle\]MON = 60° . OR = 7 cm, and OM = 21 cm. Find the lengths of arc RXQ and arc MYN. (\[\pi = \frac{22}{7}\])
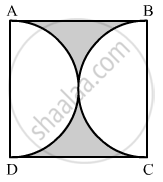
In the given figure, find the area of the shaded region, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
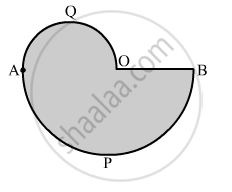
In the given figure, APB and AQO are semicircles and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region.
The perimeter of the quadrant of a circle is 25 cm. Find its area.
A wire is in the form of a circle of radius 42 cm. It is bent into a square.
Determine the side of the square and compare the area of the regions enclosed in two cases.
Find the area and perimeter of the following sector :
Diameter = 42 cm, angle at the centre is 100·.
The circumferences of two circles are in the ratio 5: 7, find the ratio between their radius.
Using a ruler and compasses only:
(i) Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ∠ ABC = 120°.
(ii) In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
(iii) Measure ∠ BCP.
A Rose garden is in the form of circle of radius 63 m. The gardener wants to fence it at the rate of ₹ 150 per metre. Find the cost of fencing?
Formula used to find the circumference of a circle is
A race track is in the form of a circular ring whose outer and inner circumferences are 396 m and 352 m respectively. The width of the track is ____________.
The radii of the two circles are 19 cm and 9 cm respectively. The radius of the circle which has a circumference equal to the sum of the circumference of two circles is ____________.
Circumferences of two circles are equal. Is it necessary that their areas be equal? Why?
Find the number of revolutions made by a circular wheel of area 1.54 m2 in rolling a distance of 176 m.
Circumference of a circle of diameter 5 cm is ______.
