Advertisements
Advertisements
प्रश्न
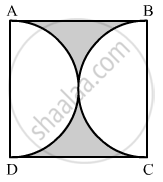
In the given figure, find the area of the shaded region, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
उत्तर
Area of the shaded region = Area of Square ABCD − (Area of semicircle APD + Area of semicircle BPC)
`=(14)^2 = [1/2 pi(14/2)^2 + 1/2pi(14/2)^2]`
`=(14)^2 - 22/7(7)^2`
= 42 cm2
Hence, the area of the shaded region is 42 cm2.
APPEARS IN
संबंधित प्रश्न
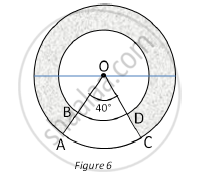
In Fig. 6, find the area of the shaded region, enclosed between two concentric circles of radii 7 cm and 14 cm where ∠AOC = 40°. (use `pi = 22/7`)
The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour. (Take π = 3.14)
A field is in the form of circle. A fence is to be erected around the field. The cost of fencing would to Rs. 2640 at rate of Rs.12 per metre. Then the field is to be thoroughs ploughed at cost of Rs. 0.50 per m2. What is amount required to plough the field?
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find Length of arc
The area of a circle is 38.5 cm2. The circumference of the circle is
The center O of a circle of a radius 1.3 cm is at a distance of 3.8 cm from a given straight line AB. Draw a circle to touch the given straight line AB at a point P so that OP = 4.7 cm and to touch the given circle externally.
Find the area of a circular field that has a circumference of 396m.
The diameter of two circles are 28 cm and 24 cm. Find the circumference of the circle having its area equal to sum of the areas of the two circles.
Find the total cost of wooden fencing around a circular garden of diameter 28 m, if 1 m of fencing costs ₹ 300.
