Advertisements
Advertisements
प्रश्न
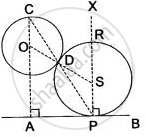
The center O of a circle of a radius 1.3 cm is at a distance of 3.8 cm from a given straight line AB. Draw a circle to touch the given straight line AB at a point P so that OP = 4.7 cm and to touch the given circle externally.
उत्तर
Steps of construction:
1) Take a point O at a distance of 3.8 cm from AB and with O as centre draw a circle of radius 1.3 cm.
2) With O as centre and radius equal to 4.7 cm, draw an arc cut BA at P. Draw PX perpendicular to AB.
3) Produce AO to cut the circle at C and join CP cutting the circle at D.
4) Join OD and produce it to cut PX at S. With S as centre and radius = SD, draw the circle PDR. This is the required circle.
APPEARS IN
संबंधित प्रश्न
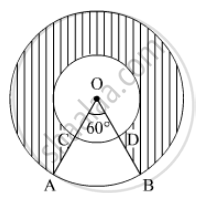
In Figure , two concentric circles with centre O, have radii 21cm and 42 cm. If ∠ AOB = 60°, find the area of the shaded region. [use π=22/7]
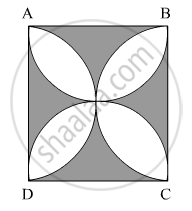
In Fig. 4, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region.
(use `pi=22/7`)
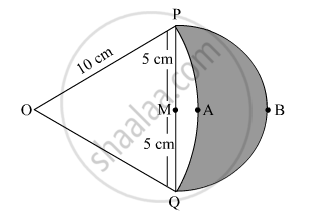
In Fig. 7, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre O and radius OP while arc PBQ is a semi-circle drawn on PQ ad diameter with centre M. If OP = PQ = 10 cm show that area of shaded region is `25(sqrt3-pi/6)cm^2`.
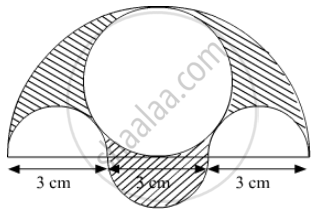
Three semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the given figure. Find the area of the shaded region
Find the angle subtended at the centre of circle of radius 5cm by an arc of length `((5pi)/3)` cm
Four equal circles, each of radius 5 cm touch each other as shown in fig. Find the area included etween them.
Find the length of the arc of a circle of diameter 42 cm which subtends an angle of 60° at the centre.
Find the area of a quadrant of a circle whose circumference is 44 cm.
The length of a chain used as the boundary of a semicircular park is 108 m. Find the area of the park.
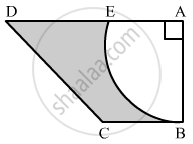
In the given figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region.
In making 1000 revolutions, a wheel covers 88 km. The diameter of the wheel is
The circumference of a circle is 22 cm. Find its area.
A circus tent is cylindrical to a height of 5 m and conical above it. If its diameter is 42 m and slant height of the cone is 53 m, calculate the total area of the canvas required.
Find the total surface area and volume of a hemisphere whose radius is 10 cm.
A wheel has a diameter of 84 cm. Find how many completer revolutions must it make to cover 3.168 km.
The circumference of a circle is eigth time the circumference of the circle with a radius of 12 cm. Find its diameter.
The radius of two circles are in the ratio 3 : 5, find the ratio between their circumferences.
Find the radius and area of the circle which has circumference equal to the sum of circumferences of the two circles of radii 3 cm and 4 cm respectively.
The area between the circumference of two concentric circles is 2464cm2. If the inner circle has a circumference of 132cm, calculate the radius of the outer circle.
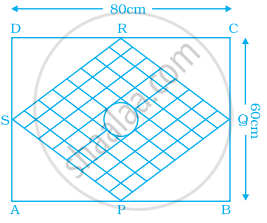
ABCD is a given rectangle with length as 80 cm and breadth as 60 cm. P, Q, R, S are the midpoints of sides AB, BC, CD, DA respectively. A circular rangoli of radius 10 cm is drawn at the centre as shown in the given figure. Find the area of shaded portion.