Advertisements
Advertisements
प्रश्न
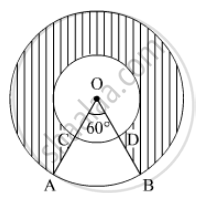
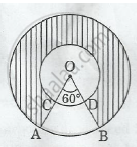
In Figure , two concentric circles with centre O, have radii 21cm and 42 cm. If ∠ AOB = 60°, find the area of the shaded region. [use π=22/7]
उत्तर १
Solution:
Given :
Radii of inner circle = 21 cm = r
Radii of outer circle = 42 cm = R
∠AOB = θ = 60°
Also,
Area of ring = π(R2-r2)
Area of a sector `= theta/360 pir^2`
The area of shaded region = Area of ring – Area of ABCD
= Area of ring – Area of sector of Outer Circle - Area of sector of Inner Circle
`=pi(R^2-r^2)-(pi(R^2-r^2))/1 xx theta/360`
`=pi(R^2-r^2)[1-theta/360]`
`=22/7(42^2-21^2)(1-60/360)`
`=3465 cm^2`
उत्तर २
Solution:
Given :
Radii of inner circle = 21 cm = r
Radii of outer circle = 42 cm = R
∠AOB = θ = 60°
Also,
Area of ring = π(R2-r2)
Area of a sector `= theta/360 pir^2`

The area of shaded region = Area of ring – Area of ABCD
= Area of ring – Area of sector of Outer Circle - Area of sector of Inner Circle
`=pi(R^2-r^2)-(pi(R^2-r^2))/1 xx theta/360`
`=pi(R^2-r^2)[1-theta/360]`
`=22/7(42^2-21^2)(1-60/360)`
`=3465 cm^2`
उत्तर ३
Given: Radius of the inner circle with radius OC, r = 21 cm
Radius of the inner circle with radius OA, R = 42 cm
∠AOB = 60°
Area of the circular ring
`= piR^2 - pir^2`
`=pi[R^2 - r^2]`
`=pi[42^2 - 21^2] cm^2`
Area of ACDB = area of sector AOB − area of COD
`= 60/360 xx pi xx R^2 - 60/300 xx pi xx r^2`
`= 60/360 xx pi[R^2 - r^2]`
`= 60/360 xx pi[42^2 - 21^2]`
Area of shaded region = area of circular ring − area of ACDB
`= pi[42^2 - 21^2] - 60/360 pi [42^2 - 21^2]`
`= pi[42^2 - 21^2][1 - 60/360]`
`= 22/7 (42 - 21) (42 + 21) xx 300/360`
`=3465 cm^2`
APPEARS IN
संबंधित प्रश्न
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150º. Find the length of its arc and area.
A car travels 1 km distance in which each wheel makes 450 complete revolutions. Find the radius of wheel.
In the given figure, OPQR is a rhombus, three of whose vertices lie on a circle with centre O. If the area of the rhombus is `32sqrt(3)`, find the radius of the circle.
The radius of a circular garden is 100 m. There is a road 10 m wide, running all around it. Find the area of the road and the cost of levelling it at Rs 20 per m2. [Use π = 3.14]
The area of a circle is 49 π cm2. Its circumference is:
In a circle of radius 14 cm, an arc subtends an angle of 120° at the centre. If `sqrt(3) = 1.73` then the area of the segment of the circle is
A 7 m road surrounds a circular garden whose area is 5544 m2. Find the area of the road and the cost of tarring it at the rate of Rs.150 per sq m.
Circumference of a circle of diameter 5 cm is ______.
The circumference of a circle whose area is 81 πr2, is ______.
