Advertisements
Advertisements
प्रश्न
In the given figure, OPQR is a rhombus, three of whose vertices lie on a circle with centre O. If the area of the rhombus is `32sqrt(3)`, find the radius of the circle.
उत्तर
In a rhombus, all sides are congruent to each other.
Thus, we have:
`"OP" = "PQ" = "QR" = "RO"`
Now, consider ΔQOP.
OQ = OP (Both are radii.)
Therefore, ΔQOP is equilateral.
similarly, ΔQOR is also euilateral and ΔQOP ≅ ΔQOR
Ar. (QROP) = Ar.( ΔQOP) + A (ΔQOP) + A(ΔQOR) = 2 Ar. [ΔQOP]
Ar. (ΔQOP) `=1/2xx32sqrt(3) = 16 sqrt(3)`
Or,
`16sqrt(3)=sqrt(3)/4"s"^2` (where s is the side of the rhombus)
Or,
s2 = 16 × 4 = 64
⇒ s = 8 cm
∴ OQ = 8 cm
Hence, the radius of the circle is 8 cm.
APPEARS IN
संबंधित प्रश्न
An arc of length 20𝜋 cm subtends an angle of 144° at centre of circle. Find the radius of the circle.
The shape of the cross section of a canal is a trapezium. If the canal is 10 m wide at the top, 6 m wide at the bottom and the area of its cross section is `640m^2` , find the depth of the canal.
The difference between the circumference and radius of a circle is 37cm. Using `pi = 22/7` , find the circumference of the circle.
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor major segments.
The wheels of the locomotive of a train are 2.1 m in radius. They make 75 revolutions in one minute.
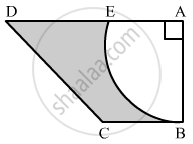
In the given figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region.
The radii of two concentric circles are 19 cm and 16 cm respectively. The area of the ring enclosed by these circles is
Find the diameter of the sphere for the following :
Surface Area = 221. 76 cm2
The circumference of a circle is eigth time the circumference of the circle with a radius of 12 cm. Find its diameter.
A circular racing track has inner circumference 528 m and outer circumference 616 m. Find the width of the track.
