Advertisements
Advertisements
Question
In the given figure, OPQR is a rhombus, three of whose vertices lie on a circle with centre O. If the area of the rhombus is `32sqrt(3)`, find the radius of the circle.
Solution
In a rhombus, all sides are congruent to each other.
Thus, we have:
`"OP" = "PQ" = "QR" = "RO"`
Now, consider ΔQOP.
OQ = OP (Both are radii.)
Therefore, ΔQOP is equilateral.
similarly, ΔQOR is also euilateral and ΔQOP ≅ ΔQOR
Ar. (QROP) = Ar.( ΔQOP) + A (ΔQOP) + A(ΔQOR) = 2 Ar. [ΔQOP]
Ar. (ΔQOP) `=1/2xx32sqrt(3) = 16 sqrt(3)`
Or,
`16sqrt(3)=sqrt(3)/4"s"^2` (where s is the side of the rhombus)
Or,
s2 = 16 × 4 = 64
⇒ s = 8 cm
∴ OQ = 8 cm
Hence, the radius of the circle is 8 cm.
APPEARS IN
RELATED QUESTIONS
In Figure, find the area of the shaded region [Use π = 3.14]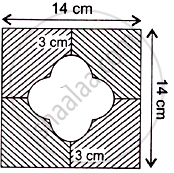
A wire is looped in the form of a circle of radius 28 cm. It is re-bent into a square form. Determine the length of the side of the square.
In Fig. there are shown sectors of two concentric circles of radii 7 cm and 3.5 cm. Find the area of the shaded region. Use π = `(\frac { 22 }{ 7 }).`
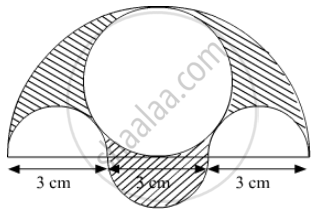
Three semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the given figure. Find the area of the shaded region
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that Perimeter of shaded region is 𝑟 (tan 𝜃 + sec 𝜃 +`(pitheta)/180`− 1)
In a circle of radius 14 cm, an arc subtends an angle of 120° at the centre. If `sqrt(3) = 1.73` then the area of the segment of the circle is
Find the volume and the surface area of the spheres in the following :
Radius= 2.1 cm
Find the area and perimeter of the following semicircles: Diameter = 7cm
Find the area of a circular field that has a circumference of 396m.
