Advertisements
Advertisements
Question
In a circle of radius 14 cm, an arc subtends an angle of 120° at the centre. If `sqrt(3) = 1.73` then the area of the segment of the circle is
Options
120.56 cm2
124.63 cm2
118.24 cm2
130.57 cm2
Solution

Radius of the circle, r = 14 cm
Draw a perpendicular OD to chord AB. It will bisect AB.
∠A = 180 - (90° + 60°) = 30°
`"cos" 30^circ = "AD"/"OA"`
`=>sqrt(3)/2 = "AD"/14`
`=>"AD" = 7sqrt(3)`
`=> "AB" = 2xx"AD"=14sqrt(3) "cm"`
`"sin" 30^circ = "OD"/14`
`=> 1/2 = "OD"/14`
⇒ OD = 7 cm
Area of minor segment = Area of sector OAPB − Area of triangle AOB
`=theta/360^circpi("OA")^2-1/2xx"OD"xx"AB"`
`=120^circ/360^circxx22/7(14)^2- 1/2xx7xx14sqrt(3)`
=205.33 - 84.77
= 120.56 cm2
Hence, the correct answer is option (a).
APPEARS IN
RELATED QUESTIONS
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square? (Take `pi = 22/7`)
A sheet of paper is in the form of rectangle ABCD in which AB = 40cm and AD = 28 cm. A semicircular portion with BC as diameter is cut off. Find the area of remaining paper.
The area of circle, inscribed in equilateral triangle is 154 cms2. Find the perimeter of
triangle.
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that
Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`
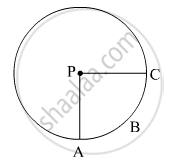
In the given figure, if A(P-ABC) = 154 cm2 radius of the circle is 14 cm, find
(1) `∠APC`
(2) l ( arc ABC) .
Find the diameter of the circle whose area is equal to the sum of the areas of two circles having radii 4 cm and 3 cm.
The sum of the radii of two circles is 7 cm, and the difference of their circumferences is 8 cm. Find the circumference of the circles.
The circumference of a circular field is 308 m. Find is:
(i) Radius
(ii) Area.
The diameter of a circular field is 56 m. Find its circumference and cost of fencing it at the rate of ₹80 per m. (Take π =`22/7`)
