Advertisements
Advertisements
Question
A sheet of paper is in the form of rectangle ABCD in which AB = 40cm and AD = 28 cm. A semicircular portion with BC as diameter is cut off. Find the area of remaining paper.
Solution
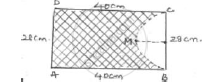
Given sheet of paper ABCD
AB = 40 cm, AD = 28 cm
⇒ CD = 40 cm, BC = 28 cm [since ABCD is rectangle]
Semicircle be represented as BMC with BC as diameter
Radius =`1/2` × 𝐵𝐶 = `1/2 × 28 = 14`𝑐𝑚𝑠
Area of remaining (shaded region) = (area of rectangle) – (area of semicircle)
= (𝐴𝐵 × 𝐵𝐶) − (`1/2` 𝜋𝑟2)
= (40 × 28) −` (1/7×22/7× 14 × 14)`
= 1120 − 308
= 812 cm2.
APPEARS IN
RELATED QUESTIONS
A car travels 1 km distance in which each wheel makes 450 complete revolutions. Find the radius of wheel.
The wheels of the locomotive of a train are 2.1 m in radius. They make 75 revolutions in one minute.
The radius of a circular garden is 100 m. There is a road 10 m wide, running all around it. Find the area of the road and the cost of levelling it at Rs 20 per m2. [Use π = 3.14]
In making 1000 revolutions, a wheel covers 88 km. The diameter of the wheel is
A hollow metallic cylindrical tube has an internal radius of 3.5 cm and height 21 cm. The thickness of the metal tube is 0.5 cm. The tube is melted and cast into a right circular cone of height 7 cm. Find the radius of the cone, correct to one decimal place.
The diameter of a circular field is 56 m. Find its circumference and cost of fencing it at the rate of ₹80 per m. (Take π =`22/7`)
The circumference of a circle is eigth time the circumference of the circle with a radius of 12 cm. Find its diameter.
The diameter of a cycle wheel is `4(5)/(11)"cm"`. How many revolutions will it make in moving 6.3km?
The area of a quadrant of a circle whose circumference is 22 cm, is ____________.
The radii of the two circles are 19 cm and 9 cm respectively. The radius of the circle which has a circumference equal to the sum of the circumference of two circles is ____________.
