Question

Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that

Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`

Answer 1

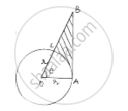
Given angle subtended at centre of circle = 𝜃

∠OAB = 90° [At joint of contact, tangent is perpendicular to radius]

OAB is right angle triangle

Cos 𝜃 =`(adj.side)/(hypotenuse) =r/OB`⇒ 𝑂𝐵 = 𝑟 sec 𝜃 … … (𝑖)

tan 𝜃 =`(opp.side)/(adju.side)=AB/r`⇒ 𝐴𝐵 = 𝑟 tan 𝜃 … … . (𝑖𝑖)

Area of shaded region = (area of triangle) – (area of sector)

`= (1/2× OA × AB) −theta/360^@× pir^2`

`=1/2× r × r tan theta −r^2/2[theta/180^@× pi]`

=`r^2/2[tantheta −(pitheta)/180]`