Advertisements
Advertisements
Question
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that Perimeter of shaded region is 𝑟 (tan 𝜃 + sec 𝜃 +`(pitheta)/180`− 1)
Solution
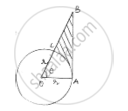
Given angle subtended at centre of circle = 𝜃
∠OAB = 90° [At joint of contact, tangent is perpendicular to radius]
OAB is right angle triangle
Cos 𝜃 =`(adj.side)/(hypotenuse) =r/OB`⇒ 𝑂𝐵 = 𝑟 sec 𝜃 … … (𝑖)
tan 𝜃 =`(opp.side)/(adju.side)=AB/r`⇒ 𝐴𝐵 = 𝑟 tan 𝜃 … … . (𝑖𝑖)
Perimeter of shaded region = AB + BC + (CA arc)
= 𝑟 tan 𝜃 + (𝑂𝐵 − 𝑂𝐶) +`theta/360^@`× 2𝜋𝑟
= 𝑟 tan 𝜃 + 𝑟 sec 𝜃 − 𝑟 +`(pithetar)/180^@`
= 𝑟 (tan 𝜃 + sec 𝜃 +`(pitheta)/180^@`− 1)
APPEARS IN
RELATED QUESTIONS
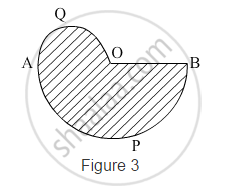
In Fig. 3, APB and AQO are semicircles, and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region [Use `pi=22/7`]
The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
Four equal circles, each of radius 5 cm touch each other as shown in fig. Find the area included etween them.
Choose the correct alternative answer for the following question.
The wheel of a motor cycle is of radius 35 cm. How many revolutions per minute must the wheel make so as to keep a speed of 66 km/hr ?
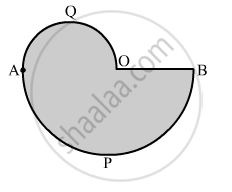
In the given figure, APB and AQO are semicircles and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region.
A wire when bent in the form of an equilateral triangle encloses an area of `121sqrt(3) "cm"^2`. The same wire is bent to form a circle. Find the area enclosed by the circle.
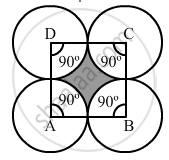
Four equal circles are described about the four corners of a square so that each touches two of the others, as shown in the figure. Find the area of the shaded region, if each side of the square measures 14 cm.
Find the diameter of the sphere for the following :
Surface Area = `576pi`cm2
Find the dimensions of a rectangular park whose perimeter is 60 m and area 200 m2.
