Question

Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that Perimeter of shaded region is 𝑟 (tan 𝜃 + sec 𝜃 +`(pitheta)/180`− 1)

Answer 1

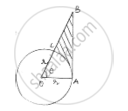
Given angle subtended at centre of circle = 𝜃

∠OAB = 90° [At joint of contact, tangent is perpendicular to radius]

OAB is right angle triangle

Cos 𝜃 =`(adj.side)/(hypotenuse) =r/OB`⇒ 𝑂𝐵 = 𝑟 sec 𝜃 … … (𝑖)

tan 𝜃 =`(opp.side)/(adju.side)=AB/r`⇒ 𝐴𝐵 = 𝑟 tan 𝜃 … … . (𝑖𝑖)

Perimeter of shaded region = AB + BC + (CA arc)

= 𝑟 tan 𝜃 + (𝑂𝐵 − 𝑂𝐶) +`theta/360^@`× 2𝜋𝑟

= 𝑟 tan 𝜃 + 𝑟 sec 𝜃 − 𝑟 +`(pithetar)/180^@`

= 𝑟 (tan 𝜃 + sec 𝜃 +`(pitheta)/180^@`− 1)