Advertisements
Advertisements
प्रश्न
Sand from a cylindrical bucket 32 cm in height and 18 cm in radius is poured onto the ground making a conical heap 24 cm high. Find the radius of the conical heap.
उत्तर
Height of the cylinder = h1 = 32 cm
Radius of bucket = r1 = 18 cm
Height of conical heap = h2 = 24 cm
Let radius of conical heap = r2
Volume of sand in the bucket = volume of sand in conical heap
⇒ `pi xx r1^2 xx h1 = 1/3 xx pi xx r2^2 xx h2`
⇒ `18 xx 18 xx 32 = 1/3 xx r2^2 xx 24`
⇒ `r2^2 = (10368 xx 3)/24`
⇒ `r2^2 = 1296`
⇒r2 = 36 cm
Radius of the conical heap = 36 cm
APPEARS IN
संबंधित प्रश्न
An elastic belt is placed around the rim of a pulley of radius 5 cm. (Fig. 10) From one point C on the belt, the elastic belt is pulled directly away from the centre O of the pulley until it is at P, 10 cm from the point O. Find the length of the belt that is still in contact with the pulley. Also find the shaded area (use π = 3.14 and `sqrt3=1.73)`

A car has wheels which are 80 cm in diameter. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour ?
If the circumference of a circular sheet is 154 m, find its radius. Also find the area of
the sheet. (Take `pi = 22/7`)
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that
Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`
Four equal circles, each of radius 5 cm touch each other as shown in fig. Find the area included etween them.
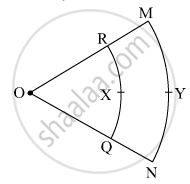
In the given figure, O is the centre of the sector. \[\angle\]ROQ = \[\angle\]MON = 60° . OR = 7 cm, and OM = 21 cm. Find the lengths of arc RXQ and arc MYN. (\[\pi = \frac{22}{7}\])
A square ABCD is inscribed in a circle of radius r. Find the area of the square.
The area of a square is the same as the area of a square. Their perimeters are in the ratio
Find the curved surface area , the total surface area and the volume of a cone if its :
Height = 8 cm , diameter = 12 cm
A wire is in the form of a circle of radius 42 cm. It is bent into a square.
Determine the side of the square and compare the area of the regions enclosed in two cases.
Find the area grazed by a horse tied with a 11. 2 m rope to a corner of a field measuring 25m by 15 m.
Find the circumference of the circle whose area is 81π cm 2.
The radius of a circle is 21 cm. Find the circumference (Take π = `3 1/7`).
The circumference of a circle is 440 cm. Find its radius and diameter. (Take π = `22/7`)
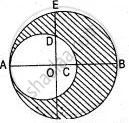
In the adjoining figure, the crescent is formed by two circles which touch at the point A. O is the centre of bigger circle. If CB = 9 cm and DE = 5 cm, find the area of the shaded portion.
Complete the table below.
| Radius (r) | Diameter (d) | Circumference (c) |
| ...... | ...... | 72.6 cm |
The radius of a circular garden is 56 m. What would it cost to put a 4-round fence around this garden at a rate of 40 rupees per metre?
Find the area and perimeter of the circles with following: Diameter = 35cm
The circumference o a garden roller is 280cm. How many revolutions does it make in moving 490m?
The diameter of the bullock cart wheel is 1.4 m. Find the distance covered by it in 150 rotations?
