Advertisements
Advertisements
प्रश्न
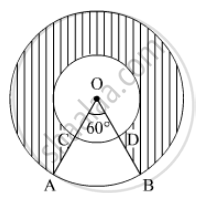
An elastic belt is placed around the rim of a pulley of radius 5 cm. (Fig. 10) From one point C on the belt, the elastic belt is pulled directly away from the centre O of the pulley until it is at P, 10 cm from the point O. Find the length of the belt that is still in contact with the pulley. Also find the shaded area (use π = 3.14 and `sqrt3=1.73)`

उत्तर

Given:
OA = 5 cm
OP = 10 cm
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore, ∆OAP is a right-angled triangle.
⇒∠OAP=90°
Now,
OP2 = OA2 + AP2
⇒ 102 = 52 + AP2
⇒ AP2 = 75
⇒ AP = 53`sqrt3 cm`
Also,
`costheta=(OA)/(OP) = 5/10`
`=>costheta=1/2`
⇒θ=60°
Now,
∠AOP=∠BOP=60° (∵∆OAP≅∆OBP)
⇒∠AOB=120°
Length of the belt still in contact with the pulley = Circumference of the circle − Length of the arc ACB
`=2xx3.14xx5-120^@/360^@xx2xx3.14xx5`
`=2xx3.14xx5xx(1-1/3)`
`=2xx3.14xx5xx2/3`
=20.93 cm (Approx.)
Now
Area of ∆OAP =
`1/2xxAPxxOA=1/2xx5sqrt3xx5=(25sqrt3)/2 cm^2`
Similarly,
Area of ∆OBP = `(25sqrt3)/2cm^2`
∴ Area of ∆OAP + Area of ∆OBP = 25`sqrt3`cm2=25×1.73=43.25 cm2
Area of sector OACB = `120^@/360^@xx3.14xx(5^2)=1/3xx3.14xx25=26.17cm^2`
∴ Area of the shaded region = (Area of ∆OAP + Area of ∆OBP) − Area of the sector OACB
= 43.25 cm2 − 26.17 cm2
= 17.08 cm2 (Approx.)
APPEARS IN
संबंधित प्रश्न
In Figure , two concentric circles with centre O, have radii 21cm and 42 cm. If ∠ AOB = 60°, find the area of the shaded region. [use π=22/7]
If the perimeter of a semi-circular protractor is 66 cm, find the diameter of the protractor (Take π = 22/7).
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find Area of the circle
The area of rhombus is `480cm^2` , and one of its diagonal measures 48 cm. Find
(i) the length of the other diagonal,
(ii) the length of each of the sides
(iii) its perimeter
A sector of 56°, cut out from a circle, contains 17.6 cm2. Find the radius of the circle.
The area of an equilateral triangle is `49sqrt(3)` cm2 . Taking each angular point as centre, circles are drawn with radius equal to half the length of the side of the triangle. Find the area of the triangle not included in the circles. [Take π = 1.73]
The diameter of a wheel is 1.4m. How many revolutions does it make in moving a distance of 2.2 kms?
Each side of a square is 44 cm. Find its perimeter. If this perimeter is equal to the circumference of a circle, find the radius of the circle.
Find the area and perimeter of the following semicircles: Radius = 1.4cm
Find the circumference of the circles whose radii are given below.
49 cm
