Advertisements
Advertisements
प्रश्न
A sector of 56°, cut out from a circle, contains 17.6 cm2. Find the radius of the circle.
उत्तर
Area of the sector = 17.6 cm2
Area of the sector`=(pi"r"^2theta)/360`
`=> 17.6 =22/7xx"r"^2xx56/360`
`=> "r"^2 = (17.6 xx7xx360)/(22xx56)`
⇒ r = 6m
∴ Radius of the circle = 6 cm
APPEARS IN
संबंधित प्रश्न
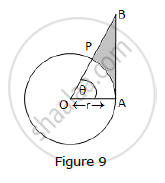
In Fig. 9, is shown a sector OAP of a circle with centre O, containing ∠θ. AB is perpendicular to the radius OQ and meets OP produced at B. Prove that the perimeter of shaded region is
`r[tantheta+sectheta+(pitheta)/180-1]`
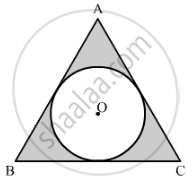
In Fig 4, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.[Use π=3.14 and √3=1.73]
The perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm. Find the area of the sector.
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find Circumference of the circle
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that
Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`
Four cows are tethered at four corners of a square plot of side 50m, so that’ they just cant reach one another. What area will be left ungrazed.
Find the curved surface area , the total surface area and the volume of a cone if its :
Height = 16 cm , diameter = 24 cm
The diameter of the bullock cart wheel is 1.4 m. Find the distance covered by it in 150 rotations?
A wheel of a car covers a distance of 3520 cm in 20 rotations. Find the radius of the wheel?
Circumference ‘C’ of a circle is equal to 2π × ______.
