Advertisements
Advertisements
प्रश्न
In Fig 4, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.[Use π=3.14 and √3=1.73]
उत्तर
It is given that ABC is an equilateral triangle of side 12 cm.
Construction:
Join OA, OB and OC.
Draw:
OP⊥BC
OQ⊥AC
OR⊥AB
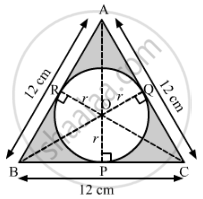
Let the radius of the circle be r cm.
Area of ∆AOB + Area of ∆BOC + Area of ∆AOC = Area of ∆ABC
`1/2xxABxxOR+1/2xxBCxxOP+1/2xxACxxOQ=sqrt3/4xx(side)^2`
`1/2xx12xxr+1/2xx12xxr+1/2xx12xxr=sqrt3/4xx(12)^2`
`3xx1/2xx12xxr=sqrt3/4xx12xx12`
`r=2sqrt3=2xx1.73=3.46`
Therefore, the radius of the inscribed circle is 3.46 cm.
Now, area of the shaded region = Area of ∆ABC − Area of the inscribed circle
`=[sqrt3/4xx(12)^2-pi(2sqrt3)^2] cm^2`
`=[36sqrt3-12pi]cm^2`
`=[36xx1.73-12xx3.14] cm^2`
`=[62.28-37.68]cm^2`
=24.6 cm2
Therefore, the area of the shaded region is 24.6 cm2
APPEARS IN
संबंधित प्रश्न
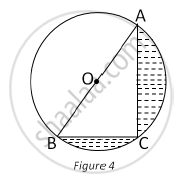
In Fig. 4, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)
Find the area of the circle if its circumfence is 88 cm.
The circumference of a garden roller is 280 cm. How many revolutions does it make in moving 490 meters?
Find the diameter of the sphere for the following :
Surface Area = 221. 76 cm2
Find the diameter of the sphere for the following :
Surface Area = `576pi`cm2
The circumference of a given circular park is 55 m. It is surrounded by a path of uniform width of 3.5 m. Find the area of the path.
The circumference of a circle is 440 cm. Find its radius and diameter. (Take π = `22/7`)
The diameter of a circular well is 4.2 m. What is its circumference?
A ground is in the form of a circle whose diameter is 350 m. An athlete makes 4 revolutions. Find the distance covered by the athlete
If the circumference of a circle is 82π, then the value of ‘r’ is
