Advertisements
Advertisements
प्रश्न
In Fig 4, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.[Use π=3.14 and √3=1.73]
उत्तर
It is given that ABC is an equilateral triangle of side 12 cm.
Construction:
Join OA, OB and OC.
Draw:
OP⊥BC
OQ⊥AC
OR⊥AB
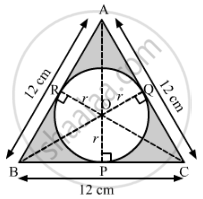
Let the radius of the circle be r cm.
Area of ∆AOB + Area of ∆BOC + Area of ∆AOC = Area of ∆ABC
`1/2xxABxxOR+1/2xxBCxxOP+1/2xxACxxOQ=sqrt3/4xx(side)^2`
`1/2xx12xxr+1/2xx12xxr+1/2xx12xxr=sqrt3/4xx(12)^2`
`3xx1/2xx12xxr=sqrt3/4xx12xx12`
`r=2sqrt3=2xx1.73=3.46`
Therefore, the radius of the inscribed circle is 3.46 cm.
Now, area of the shaded region = Area of ∆ABC − Area of the inscribed circle
`=[sqrt3/4xx(12)^2-pi(2sqrt3)^2] cm^2`
`=[36sqrt3-12pi]cm^2`
`=[36xx1.73-12xx3.14] cm^2`
`=[62.28-37.68]cm^2`
=24.6 cm2
Therefore, the area of the shaded region is 24.6 cm2
APPEARS IN
संबंधित प्रश्न
A car travels 1 km distance in which each wheel makes 450 complete revolutions. Find the radius of wheel.
The perimeter of a rhombus is 60 cm. If one of its diagonal us 18 cm long, find
(i) the length of the other diagonal, and
(ii) the area of the rhombus.
Find the area of the sector of a circle having radius 6 cm and of angle 30°. [Take π = 3.14]
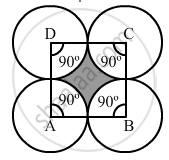
Four equal circles are described about the four corners of a square so that each touches two of the others, as shown in the figure. Find the area of the shaded region, if each side of the square measures 14 cm.
The area of a circle is 38.5 cm2. The circumference of the circle is
Find the area enclosed between two concentric circles, if their radii are 6 cm and 13 cm respectively.
Find the area grazed by a horse tied with a 11. 2 m rope to a corner of a field measuring 25m by 15 m.
Find the area and perimeter of the following semicircles: Radius = 1.4cm
A bucket is raised from a well by means of a rope wound round a wheel of diameter 35 cm. If the bucket ascends in 2 minutes with a uniform speed of 1.1 m per sec, calculate the number of complete revolutions the wheel makes in raising the bucket.
The cost of fencing a circular race course at the rate of ₹ 8 per metre is ₹ 2112. Find the diameter of the race course
