Advertisements
Advertisements
प्रश्न
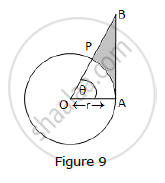
In Fig. 9, is shown a sector OAP of a circle with centre O, containing ∠θ. AB is perpendicular to the radius OQ and meets OP produced at B. Prove that the perimeter of shaded region is
`r[tantheta+sectheta+(pitheta)/180-1]`
उत्तर
Perimeter of shaded region = AB + PB + arc length AP...(1)
Arc length AP = `theta/360xx2pir=(pithetar)/180" ....(2)"`
In right angled ΔOAB,
`tan theta=(AB)/r=>AB=rtan theta" ....(3)"`
`sec theta=(OB)/r =>OB=rsec theta`
OB = OP + PB
∴ r secθ=r+PB
∴ PB = r secθ - r.....(4)
Substitute (2), (3) and (4) in (1), we get
Perimeter of shaded region = AB+PB+ arc length AP
`=rtantheta+rsectheta-r+(pithetar)/180`
`=r[tantheta+sec theta+(pitheta)/180-1]`
APPEARS IN
संबंधित प्रश्न
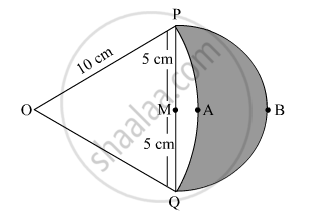
In Fig. 7, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre O and radius OP while arc PBQ is a semi-circle drawn on PQ ad diameter with centre M. If OP = PQ = 10 cm show that area of shaded region is `25(sqrt3-pi/6)cm^2`.
The base of a right – angled triangle measures 48 cm and its hypotenuse measures 50 cm. Find the area of the triangle.
Choose the correct alternative answer for the following question.
Find the curved surface area , the total surface area and the volume of a cone if its :
Height = 8 cm , diameter = 12 cm
Find the volume and the surface area of the spheres in the following :
Radius = 7 cm
A cylindrical bucket, whose base radius is 20 cm, is filled with water to a height of 25 cm. A heavy iron spherical ball of radius 10 cm is dropped to submerge completely in water in the bucket. Find the increase in the level of water.
Draw the circumcircle of Δ PMT in which PM = 5.4, P = 60°, M = 70°.
A wire when bent in the form of a square encloses an area of 484cm2. If the same wire is bent into the form of a circle, find the area of the circle.
In a circle of diameter 42 cm, if an arc subtends an angle of 60° at the centre, where `pi = 22/7` then length of an arc is ____________.
The numerical value of the area of a circle is greater than the numerical value of its circumference. Is this statement true? Why?
