Advertisements
Advertisements
प्रश्न
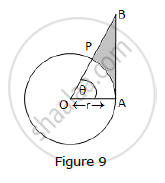
In Fig. 9, is shown a sector OAP of a circle with centre O, containing ∠θ. AB is perpendicular to the radius OQ and meets OP produced at B. Prove that the perimeter of shaded region is
`r[tantheta+sectheta+(pitheta)/180-1]`
उत्तर
Perimeter of shaded region = AB + PB + arc length AP...(1)
Arc length AP = `theta/360xx2pir=(pithetar)/180" ....(2)"`
In right angled ΔOAB,
`tan theta=(AB)/r=>AB=rtan theta" ....(3)"`
`sec theta=(OB)/r =>OB=rsec theta`
OB = OP + PB
∴ r secθ=r+PB
∴ PB = r secθ - r.....(4)
Substitute (2), (3) and (4) in (1), we get
Perimeter of shaded region = AB+PB+ arc length AP
`=rtantheta+rsectheta-r+(pithetar)/180`
`=r[tantheta+sec theta+(pitheta)/180-1]`
APPEARS IN
संबंधित प्रश्न
Four equal circles each of radius a, touch each other. Show that area between them is `6/7a^2`
The radius of a sector of a circle is 7 cm. If the measure of the arc of the sector is - three right angles; find the area of the sector in case.
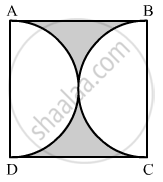
In the given figure, find the area of the shaded region, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
The wheels of a car make 2500 revolutions in covering a distance of 4.95 km. Find the diameter of a wheel.
The radii of two circles are 48 cm and 13 cm. Find the area of the circle which has its circumference equal to the difference of the circumferences of the given two circles.
Find the area and perimeter of the circles with following: Radius = 10.5cm
The circumference o a garden roller is 280cm. How many revolutions does it make in moving 490m?
A 4.2m wide road surrounds a circular plot whose circumference is 176m. Find the cost of paving the road at Rs.75per m2.
The perimeter of a sector of radius 5.2 cm is 16.4 cm, the area of the sector is ____________.
A photograph of Billiard/Snooker table has dimensions as `1/10`th of its actual size as shown in the given figure:
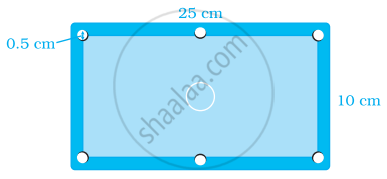
The portion excluding six holes each of diameter 0.5 cm needs to be polished at rate of ₹ 200 per m2. Find the cost of polishing.
