Advertisements
Advertisements
प्रश्न
Four equal circles each of radius a, touch each other. Show that area between them is `6/7a^2`
उत्तर
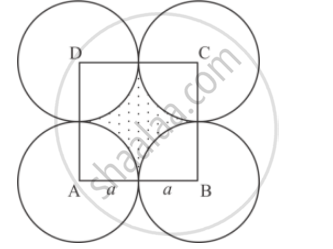
Let circles be with centres A, B, C, D]
Join A, B, C and D then ABCD is square formed with side = (a + a) = 2a
Radius = a
Area between circles = area of square – 4(area of quadrant)
(shaded region)
= (2𝑎)2 − 4 (`1/4`𝑎𝑟𝑒𝑎 𝑜𝑓 𝑐𝑖𝑟𝑐𝑙𝑒 𝑤𝑖𝑡ℎ 𝑟𝑎𝑑𝑖𝑢𝑠 ′𝑎′)
=` 4a^2 − 4 (1/4) × a^2`
= 𝑎2(4 − 𝜋)
= 𝑎2 (4 −`22/7`)
= `((28−22)/7) a^2 =6/7a^2`
∴ Area between circles =`6/7a^2.`
APPEARS IN
संबंधित प्रश्न
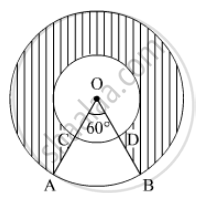
In Figure , two concentric circles with centre O, have radii 21cm and 42 cm. If ∠ AOB = 60°, find the area of the shaded region. [use π=22/7]
The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days. (Take π = 22/7)
The circumference of two circles are in ratio 2:3. Find the ratio of their areas
A road which is 7m wide surrounds a circular park whose circumference is 352m. Find the area of road.
The base of a right – angled triangle measures 48 cm and its hypotenuse measures 50 cm. Find the area of the triangle.
In the given figure, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region. [π = 3.14]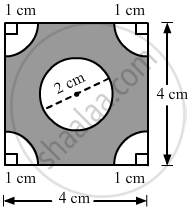
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the area of the minor and major segments.
A lawn is in the shape of a semi-circle of diameter 42 m. The lawn is surrounded by a flower bed of width 7 m all around. Find the area of the flower bed in m2 .
The circumference of a circular field is 308 m. Find is:
(i) Radius
(ii) Area.
The cost of decorating the circumference of a circular lawn of a house at the rate of ₹ 55 per metre is ₹ 16940. What is the radius of the lawn?
