Question

Four equal circles each of radius a, touch each other. Show that area between them is `6/7a^2`

Answer 1

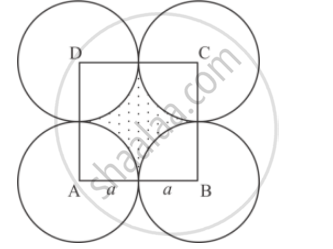
Let circles be with centres A, B, C, D]

Join A, B, C and D then ABCD is square formed with side = (a + a) = 2a

Radius = a

Area between circles = area of square – 4(area of quadrant)

(shaded region)

= (2𝑎)² − 4 (`1/4`𝑎𝑟𝑒𝑎 𝑜𝑓 𝑐𝑖𝑟𝑐𝑙𝑒 𝑤𝑖𝑡ℎ 𝑟𝑎𝑑𝑖𝑢𝑠 ′𝑎′)

=` 4a^2 − 4 (1/4) × a^2`

= 𝑎²(4 − 𝜋)

= 𝑎² (4 −`22/7`)
= `((28−22)/7) a^2 =6/7a^2`
∴ Area between circles =`6/7a^2.`