Advertisements
Advertisements
Question
Four equal circles each of radius a, touch each other. Show that area between them is `6/7a^2`
Solution
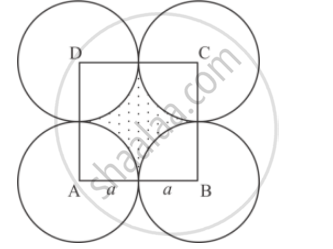
Let circles be with centres A, B, C, D]
Join A, B, C and D then ABCD is square formed with side = (a + a) = 2a
Radius = a
Area between circles = area of square – 4(area of quadrant)
(shaded region)
= (2๐)2 − 4 (`1/4`๐๐๐๐ ๐๐ ๐๐๐๐๐๐ ๐ค๐๐กโ ๐๐๐๐๐ข๐ ′๐′)
=` 4a^2 − 4 (1/4) × a^2`
= ๐2(4 − ๐)
= ๐2 (4 −`22/7`)
= `((28−22)/7) a^2 =6/7a^2`
∴ Area between circles =`6/7a^2.`
APPEARS IN
RELATED QUESTIONS
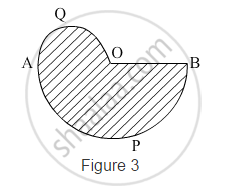
In Fig. 3, APB and AQO are semicircles, and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region [Use `pi=22/7`]
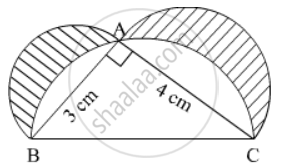
In the given figure, โ ABC is a right-angled triangle in which ∠ A is 90°. Semicircles are drawn on AB, AC and BC as diameters. Find the area of the shaded region
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find Area of the circle
A horse is placed for grazing inside a rectangular field 70 m by 52 m. It is tethered to one corner by a rope 21 m long. On how much area can it graze? How much area is left ungrazed?
Three equal circles, each of radius 6 cm, touch one another as shown in the figure. Find the area of enclosed between them.
The sum of the circumference and diameter of a circle is 116 cm. Find its radius.
The diameter of a circular field is 56 m. Find its circumference and cost of fencing it at the rate of โน80 per m. (Take π =`22/7`)
Ratio of circumference of a circle to its radius is always 2π:I.
A circle with radius 16 cm is cut into four equal parts and rearranged to form another shape as shown in the below figure:
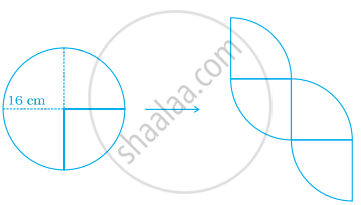
Does the perimeter change? If it does change, by how much does it increase or decrease?
The circumferences of two circles are in the ratio 4 : 5. What is the ratio of their radii?
