Advertisements
Advertisements
Question
A horse is placed for grazing inside a rectangular field 70 m by 52 m. It is tethered to one corner by a rope 21 m long. On how much area can it graze? How much area is left ungrazed?
Solution
Radius of the quadrant of the circle = 21 m
The shaded portion shows the part of the field the horse can graze.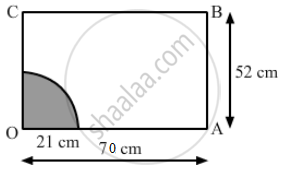
Area of the grazed field = Area of the quadrant OPQ
`=1/4` of the circle having radius OP
`=1/4pi"r"^2`
`=1/4xxpi"r"^2`
`= 1/4 xx 22/7xx21xx21`
= 346.5 m2
Total area of the field = 70 × 52 = 3640 m2
Area left ungrazed = Area of the field -- Area of the grazed field
= 3640 - 346.5 = 3293.5 m2
APPEARS IN
RELATED QUESTIONS
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that
Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`
A plot is in the form of rectangle ABCD having semi-circle on BC. If AB = 60m and BC = 28m, find the area of plot.
A copper wire when bent in the form of a square encloses an area of 484 cm2. The same wire is not bent in the form of a circle. Find the area enclosed by the circle.
A boy is cycling in such a way that the wheels of his bicycle are making 140 revolutions per minute. If the diameter of a wheel is 60 cm, calculate the speed (in km/h) at which the boy is cycling.
The perimeter of a circular field is 242 m. The area of the field is
The radii of two concentric circles are 19 cm and 16 cm respectively. The area of the ring enclosed by these circles is
The diameter of a circle is 5.6 cm. Find its circumference.
A bucket is raised from a well by means of a rope wound round a wheel of diameter 35 cm. If the bucket ascends in 2 minutes with a uniform speed of 1.1 m per sec, calculate the number of complete revolutions the wheel makes in raising the bucket.
Find the circumference of the circles whose radii are given below.
91 mm
The area of a circular playground is 22176 m2. Find the cost of fencing this ground at the rate of Rs 50 per metre.
