Advertisements
Advertisements
Question
A boy is cycling in such a way that the wheels of his bicycle are making 140 revolutions per minute. If the diameter of a wheel is 60 cm, calculate the speed (in km/h) at which the boy is cycling.
Solution
Diameter of the wheel = 60 cm
∴ Radius of the wheel = 30 cm
circumference of the wheel = 2πr
`=2xx22/7xx30`
`= 1320/7 "cm"`
Distance covered by the wheel in 1 revolution `= 1320/7 "cm"`
∴ Distance covered by the wheel in 140 revolutions`=(1320/7xx140xx1/100) "m"`
`=((1320xx140)/(7xx1000)xx1/100) "Km"= 264/1000 "Km"`
Now,
Distance covered by the wheel in 1 minute = Distance covered by the wheel in 140 revolutions `= 264/1000 "km"`
∴ Distance covered by the wheel in 1 hour `=264/1000xx60=15.84 "Km" //"h"`
Hence, the speed at which the boy is cycling is 15.84 km/h.
APPEARS IN
RELATED QUESTIONS
A wire is looped in the form of a circle of radius 28 cm. It is re-bent into a square form. Determine the length of the side of the square.
The sum of the radii of two circles is 140 cm and the difference of their circumferences in 88 cm. Find the diameters of the circles.
The circumference of a circle is 8 cm. Find the area of the sector whose central angle is 72°.
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor major segments.
The perimeter of a circular field is 242 m. The area of the field is
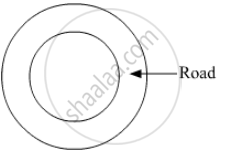
Diameter of the circular garden is 42 m. There is a 3.5 m wide road around the garden. Find the area of the road.
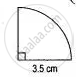
In the adjoining figure, the radius is 3.5 cm. Find:
(i) The area of the quarter of the circle correct to one decimal place.
(ii) The perimeter of the quarter of the circle correct to one decimal place. ( Take π = `22/7`)
The wheel of a bullock cart has a diameter of 1.4 m. How many rotations will the wheel complete as the cart travels 1.1 km?
Find the area and perimeter of the following semicircles: Diameter = 5.6cm
Find the perimeter of the given shape (Take π = `22/7`).