Advertisements
Advertisements
Question
The diameter of the wheels of a bus is 140 cm. How many revolutions per minute do the wheels make when the bus is moving at a speed of 72.6 km per hour?
Solution
Diameter of the wheel = 140 cm
Radius = 70 cm
Circumference = 2πr
`=2xx22/7xx70`
= 440 cm
Speed of the wheel = 72.6 km per hour
Distance covered by the wheel in 1 minute `=(72.6xx1000xx100)/60 = 121000 "cm"`
Number of revolutions made by the wheel in 1 minute` ="Total distance covered"/"Circumference"`
`=121000/440`
= 275
Hence, the wheel makes 275 revolutions per minute.
APPEARS IN
RELATED QUESTIONS
Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15/m2. (Take π = 3.14)
A square of diagonal 8 cm is inscribed in a circle. Find the area of the region lying outside the circle and inside the square.
Find the area of the circle in which a square of area 64 cm2 is inscribed. [Use π = 3.14]
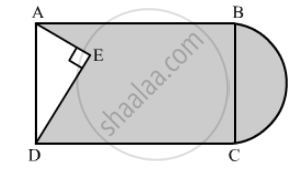
In the following figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π =]`22/7` [CBSE 2014]
The perimeter of the sector OAB shown in the following figure, is

If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then its radius is
The perimeter of a certain sector of a circle of radius 6.5 cm in 31 cm. Find the area of the sector.
The sum of the radii of two circles is 10.5 cm and the difference of their circumferences is 13.2 cm. Find the radii of the two circles.
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is ______.
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of radii 40cm and 9cm?
