Advertisements
Advertisements
प्रश्न
The diameter of the wheels of a bus is 140 cm. How many revolutions per minute do the wheels make when the bus is moving at a speed of 72.6 km per hour?
उत्तर
Diameter of the wheel = 140 cm
Radius = 70 cm
Circumference = 2πr
`=2xx22/7xx70`
= 440 cm
Speed of the wheel = 72.6 km per hour
Distance covered by the wheel in 1 minute `=(72.6xx1000xx100)/60 = 121000 "cm"`
Number of revolutions made by the wheel in 1 minute` ="Total distance covered"/"Circumference"`
`=121000/440`
= 275
Hence, the wheel makes 275 revolutions per minute.
APPEARS IN
संबंधित प्रश्न
The area of rectangle is `192cm^2` and its perimeter is 56 cm. Find the dimensions of the rectangle.
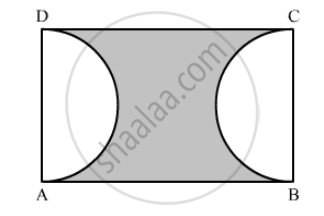
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the length of the boundary of the shaded region.
What is the area of a sector of a circle of radius 5 cm formed by an arc of length 3.5 cm?
A wire can be bent in the form of a circle of radius 56 cm. If it is bent in the form fo a square, then its area will be
If AB is a chord of length \[5\sqrt{3}\] cm of a circle with centre O and radius 5 cm, then area of sector OAB is
A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
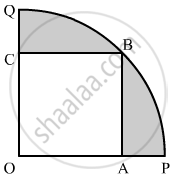
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the length of the arc and the area of the sector.
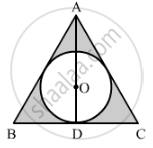
In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.
[Use `sqrt(3)= 1.73, pi = 3.14]`
Perimeter of a sector of a circle whose central angle is 90° and radius 7 cm is ____________.
