Advertisements
Advertisements
प्रश्न
The area of rectangle is `192cm^2` and its perimeter is 56 cm. Find the dimensions of the rectangle.
उत्तर
Area of the rectangle `192 cm^2`
Perimeter of the rectangle 56 cm
Perimeter = 2(length + breath)
⇒`56=2(l+b)`
⇒`l+b=28`
⇒` l=28-b`
`"Area"="Length" xx "breath"`
⇒`192=(28-b)xb`
⇒`192=28b-b^2`
⇒`b^2-28b+192=0`
⇒`(b-16) (b-12)=0`
⇒` b=16 or 12`
Thus, we have;
`l=28-12`
⇒`l=28-12`
⇒` l=16`
We will take length as 16 cm and breath as 12 cm because length is greater than breath by convention.
APPEARS IN
संबंधित प्रश्न
Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15/m2. (Take π = 3.14)
The base of an isosceles triangle measures 80 cm and its area is 2 `360 . cm^2` Find the perimeter of the triangle.
The length of a rectangular park is twice its breadth and its perimeter is 840 m. Find the area of the park.
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of the sector of the circle formed by chord AB.
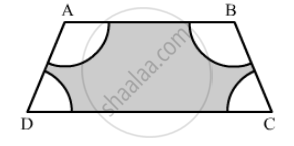
In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm DC = 32 cm and the distance between AB and DC is 14 cm. Circles of equal radii 7 cm with centres A, B, C and D have been drawn. Then find the area of the shaded region.
(Use \[\pi = \frac{22}{7}\]
If π is taken as `22/7` the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is
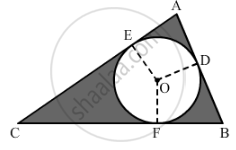
In the given figure, ∆ABC is right-angled at A. Find the area of the shaded region if AB = 6 cm, BC = 10 cm and O is the centre of the incircle of ∆ABC.
The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.
The following figure shows two circles with the same center. The radius of the larger circle is 10 cm and the radius of the smaller circle is 4 cm.

Find:
(a) the area of the larger circle
(b) the area of the smaller circle
(c) the shaded area between the two circles. (π = 3.14)
A table top is semicircular in shape with diameter 2.8 m. Area of this table top is ______.
