Advertisements
Advertisements
प्रश्न
If π is taken as `22/7` the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is
विकल्प
2.2
1.1
9.625
96.25
उत्तर
Diameter of wheel (d) = 35 cm
Radius of wheel (r) = `"d"/2 = 35/2` cm
∴ The distance covered by the wheel in 1 revolution is equal to the circumference of the wheel = 2πr
= `2 × 22/7 × 35/2`
= `cancel2 × 22/(cancel(7)1) × (cancel(35)5)/cancel2`
= 22 × 5
= 110 cm
The distance covered by the wheel in one revolution (in m) is given by = `110/100` = 1.1 m
APPEARS IN
संबंधित प्रश्न
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB=90° and AC = 15 cm.

In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
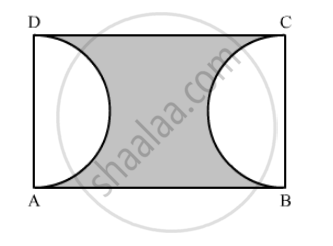
In the following figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14).
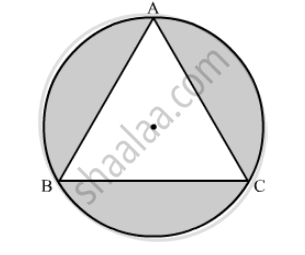
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
ABCD is a square of side 4 cm. If E is a point in the interior of the square such that ΔCEDis equilateral, then area of Δ ACE is
A circular disc of radius 6 cm is divided into three sectors with central angles 90°,120° and 150°. What part of the whole circle is the sector with central angle 150°? Also, calculate the ratio of the areas of the three sectors.
The radius of a wheel is 0.25 m. How many revolutions will it make in covering 11 km?
In the given figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.
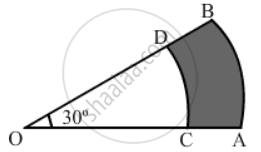
The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.
A table top is semicircular in shape with diameter 2.8 m. Area of this table top is ______.
