Advertisements
Advertisements
प्रश्न
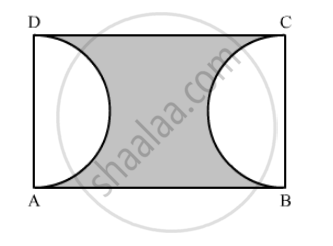
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
उत्तर
We have given two semi-circles and a rectangle.
Area of the shaded region = Area of the rectangle − Area of the two semicircles
`∴ "Area of the shaded region" =20xx14-2xx1/2xxpixx7xx7`
Substituting pi=`22/7` we get,
`∴ "Area of the shaded region"=20xx14-2xx1/2xx22/7xx7xx7`
`∴ "Area of the shaded region"=20xx14-22xx7`
`∴ "Area of the shaded region"280-154`
`∴ "Area of the shaded region"=126`
Therefore, area of shaded region is `126 cm^2`
APPEARS IN
संबंधित प्रश्न
The perimeter of a rectangular plot of land is 80 m and its breadth is 16 m. Find the length and area of the plot.
A 80 m by 64 m rectangular lawn has two roads, each 5 m wide, running through its middle, one parallel to its length and the other parallel to its breadth. Find the cost of gravelling the reads at ₹` 40 per m^2`
Prove that the area of a circular path of uniform width h surrounding a circular region of radius r is `pih(2r+h)`
If the diameter of a semi-circular protractor is 14 cm, then find its perimeter.
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then its radius is
Find the lengths of the arcs cut off from a circle of radius 12 cm by a chord 12 cm long. Also, find the area of the minor segment.
Find the areas of both the segments of a circle of radius 42 cm with central angle 120°.
If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
A circle of the largest area is cut from a rectangular piece of cardboard with dimensions 55 cm and 42 cm. Find the ratio between the area of the circle cut and the area of the remaining card-board.
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

