Advertisements
Advertisements
प्रश्न
Find the areas of both the segments of a circle of radius 42 cm with central angle 120°.
उत्तर
Area of the minor sector`=120/360xxpixx42xx42`
`=1/3xxpixx42xx42xx42`
`= pixx14xx42`
= 18488 cm2
Area of the triangle `= 1/2 "R"^2sin theta`
Here, R is the measure of the equal sides of the isosceles triangle and θ is the angle enclosed by the equal sides.
Thus, we have;
`1/2xx42xx42xxsin(120^circ)`
= 762.93 cm2
Area of the minor segment = Area of the sector - Area of the triangle
= 1848 - 762.93 = 1085.07 cn
Area of the major segment = Area of the circle - Area of the minor segment
=(π × 42 × 42)- 1085.07
= 5544 - 1085.07
=4458.93 cm2
APPEARS IN
संबंधित प्रश्न
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of the sector of the circle formed by chord AB.
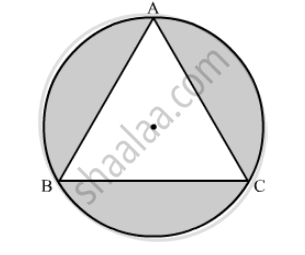
In the following figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14).
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
The area of the incircle of an equilateral triangle of side 42 cm is
The perimeter of a triangle is 30 cm and the circumference of its incircle is 88 cm. The area of the triangle is
If the sum of the areas of two circles with radii r1 and r2 is equal to the area of a circle of radius r, then \[r_1^2 + r_2^2\]
The area of the circle that can be inscribed in a square of side 10 cm is
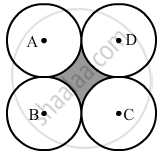
Four equal circles, each of radius 5 cm, touch each other, as shown in the figure. Find the area included between them.
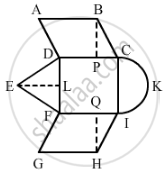
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
Calculate the area of the shotput circle whose radius is 2.135 m.
