Advertisements
Advertisements
प्रश्न
Find the areas of both the segments of a circle of radius 42 cm with central angle 120°.
उत्तर
Area of the minor sector`=120/360xxpixx42xx42`
`=1/3xxpixx42xx42xx42`
`= pixx14xx42`
= 18488 cm2
Area of the triangle `= 1/2 "R"^2sin theta`
Here, R is the measure of the equal sides of the isosceles triangle and θ is the angle enclosed by the equal sides.
Thus, we have;
`1/2xx42xx42xxsin(120^circ)`
= 762.93 cm2
Area of the minor segment = Area of the sector - Area of the triangle
= 1848 - 762.93 = 1085.07 cn
Area of the major segment = Area of the circle - Area of the minor segment
=(π × 42 × 42)- 1085.07
= 5544 - 1085.07
=4458.93 cm2
APPEARS IN
संबंधित प्रश्न
The cost of harvesting a square field at ₹ 900 per hectare is ₹ 8100. Find the cost of putting a fence around it at ₹ 18 per meter.
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
How many revolutions a circular wheel of radius r metres makes in covering a distance of s metres?
The minute hand of a clock is 15 cm long. Calculate the area swept by it in 20 minutes.
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made.
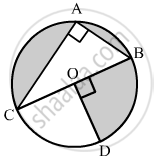
In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of shaded region.
The radius of a wheel is 0.25 m. How many revolutions will it make in covering 11 km?
Find the area enclosed between two concentric circles of radii 6.3cm and 8.4cm. A third concentric circle is drawn outside the 8.4cm circle. So that the area enclosed between it and the 8.4cm circle is the same as that between the two inner circles. Find the radii of the third circle correct to two decimal places.
In a grassland, a sheep is tethered by a rope of length 4.9 m. Find the maximum area that the sheep can graze
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (Use π = 3.14).