Advertisements
Advertisements
प्रश्न
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor major segments.
उत्तर
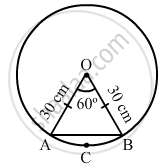
Let the chord be AB. The ends of the chord are connected to the centre of the circle O to give the triangle OAB.
OAB is an isosceles triangle. The angle at the centre is 60°
Area of the triangle `=1/2(30)^2 sin 60^circ = 450xxsqrt(3)/2 = 389.25 "cm"^2`
Area of the sector OACBO` =60/360xxpixx30xx30 = 150pi = 471 "cm"^2`
Area of the minor segment = Area of the sector - Area of the minor segment
= (π × 30 × 30) - 81.29
= 2744.71 cm2
APPEARS IN
संबंधित प्रश्न
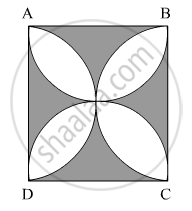
In Fig. 4, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region.
(use `pi=22/7`)
A field is in the form of circle. A fence is to be erected around the field. The cost of fencing would to Rs. 2640 at rate of Rs.12 per metre. Then the field is to be thoroughs ploughed at cost of Rs. 0.50 per m2. What is amount required to plough the field?
Find the area of a right – angled triangle, the radius of whose, circumference measures 8 cm and the altitude drawn to the hypotenuse measures 6 cm.
Find the area and perimeter of the circle with the following :
Radius= 10.5 cm
A wire bent in the form of an equilateral triangle has an area of 121 `sqrt 3` cm2. If the same wire is bent into the form of a circle , find the area enclosed by the wire.
The sum of the circumference and diameter of a circle is 116 cm. Find its radius.
Find the area and perimeter of the circles with following: Radius = 2.8cm
The radius of a circular plot is 7.7 metres. How much will it cost to fence the plot with 3 rounds of wire at the rate of 50 rupees per metre?
In the formula, C = 2πr, ‘r’ refers to
In covering a distance s metres, a circular wheel of radius r metres makes `s/(2πr)` revolutions. Is this statement true? Why?
