Advertisements
Advertisements
प्रश्न
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor major segments.
उत्तर
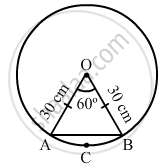
Let the chord be AB. The ends of the chord are connected to the centre of the circle O to give the triangle OAB.
OAB is an isosceles triangle. The angle at the centre is 60°
Area of the triangle `=1/2(30)^2 sin 60^circ = 450xxsqrt(3)/2 = 389.25 "cm"^2`
Area of the sector OACBO` =60/360xxpixx30xx30 = 150pi = 471 "cm"^2`
Area of the minor segment = Area of the sector - Area of the minor segment
= (π × 30 × 30) - 81.29
= 2744.71 cm2
APPEARS IN
संबंधित प्रश्न
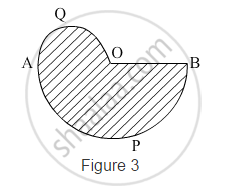
In Fig. 3, APB and AQO are semicircles, and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region [Use `pi=22/7`]
A rectangular piece is 20m long and 15m wide from its four corners, quadrants of 3.5m radius have been cut. Find the area of remaining part.
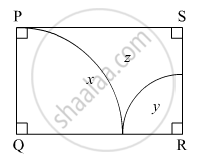
In the given figure,
\[\square\] PQRS is a rectangle. If PQ = 14 cm, QR = 21 cm, find the areas of the parts x, y, and z.
Choose the correct alternative answer for the following question.
In the given figure, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region. [π = 3.14]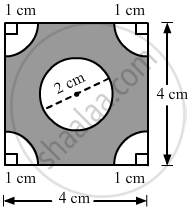
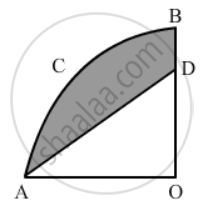
OACB is a quadrant of a circle with centre O and its radius is 3.5 cm. If OD = 2 cm. find the area of
- quadrant OACB
- the shaded region.
Find the diameter of the sphere for the following :
Volume = `72pi "cm"^3`
The radii of two circles are 25 cm and 18 cm. Find the radius of the circle which has a circumference equal to the sum of circumferences of these two circles.
The circumference of a circle is eigth time the circumference of the circle with a radius of 12 cm. Find its diameter.
In a circle of diameter 42 cm, if an arc subtends an angle of 60° at the centre, where `pi = 22/7` then length of an arc is ____________.
