Advertisements
Advertisements
प्रश्न
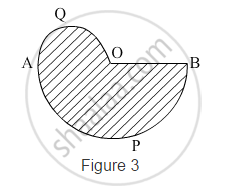
In Fig. 3, APB and AQO are semicircles, and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region [Use `pi=22/7`]
उत्तर
Let the radius of the semi-circle APB be r
⇒ The radius of the semi-circle AQO =`r/2`
Now,
Perimeter of the given figure = Length of arc AQO + Length of arc APB + OB
`=pixxr/2+pixxr+r`
`=r(3/2pi+1)`
`=r(3/2xx22/7+1)`
`= r((33+7)/7)`
`=r(40/7)cm`
⇒r=7 cm
∴ Area of the shaded region = Area of semi-circle AQO + Area of semi-circle APB
`=(pi(r/2)^2)/2+(pir^2)/2`
`=(pi(7/2)^2)/2+(pixx7^2)/2`
`=(49pi)/8+(49pi)/2`
`=49pi(1/8+1/2)`
`=49xx22/7xx5/8`
= 96.25 cm2
APPEARS IN
संबंधित प्रश्न
The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days. (Take π = 22/7)
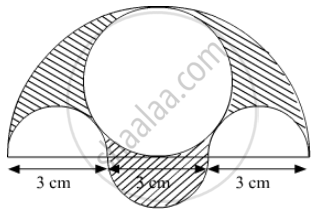
Three semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the given figure. Find the area of the shaded region
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that
Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`
The difference between the circumference and radius of a circle is 37cm. Using `pi = 22/7` , find the circumference of the circle.
The radii of two circles are 19 cm and 9 cm, Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
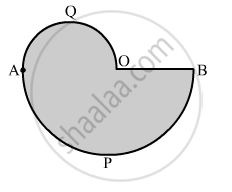
In the given figure, APB and AQO are semicircles and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region.
The area between the circumferences of two concentric circles is 2464 cm2. If the inner circle has circumference of 132 cm, calculate the radius of outer circle.
Using a ruler and compasses only:
(i) Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ∠ ABC = 120°.
(ii) In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
(iii) Measure ∠ BCP.
Areas of two circles are equal. Is it necessary that their circumferences are equal? Why?
Circumference of a circle of diameter 5 cm is ______.
