Advertisements
Advertisements
प्रश्न
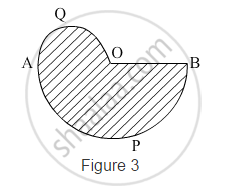
In Fig. 3, APB and AQO are semicircles, and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region [Use `pi=22/7`]
उत्तर
Let the radius of the semi-circle APB be r
⇒ The radius of the semi-circle AQO =`r/2`
Now,
Perimeter of the given figure = Length of arc AQO + Length of arc APB + OB
`=pixxr/2+pixxr+r`
`=r(3/2pi+1)`
`=r(3/2xx22/7+1)`
`= r((33+7)/7)`
`=r(40/7)cm`
⇒r=7 cm
∴ Area of the shaded region = Area of semi-circle AQO + Area of semi-circle APB
`=(pi(r/2)^2)/2+(pir^2)/2`
`=(pi(7/2)^2)/2+(pixx7^2)/2`
`=(49pi)/8+(49pi)/2`
`=49pi(1/8+1/2)`
`=49xx22/7xx5/8`
= 96.25 cm2
APPEARS IN
संबंधित प्रश्न
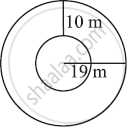
Find the circumference of the inner and the outer circles, shown in the adjoining figure? (Take π = 3.14)
A sector of 56°, cut out from a circle, contains 17.6 cm2. Find the radius of the circle.
The circumference of a circle is 39.6 cm. Find its area.
OACB is a quadrant of a circle with centre O and its radius is 3.5 cm. If OD = 2 cm. find the area of
- quadrant OACB
- the shaded region.
Find the circumference of the circle whose area is 25 times the area of the circle with radius 7 cm.
The circumference of a circle is equal to the perimeter of a square. The area of the square is 484 sq. m. Find the area of the circle.
The diameter of a wheel is 1.4m. How many revolutions does it make in moving a distance of 2.2 kms?
Find the volume and the surface area of the spheres in the following :
Radius= 2.1 cm
Find the radius of the circle whose circumference is equal to the sum of the circumferences of the circles having radius 15 cm and 8 cm.
AC and BD are two perpendicular diameter of a circle ABCD. Given that the area of shaded portion is 308 cm2 calculate:
(i) The length of AC and
(ii) The circumference of circle