Advertisements
Advertisements
Question
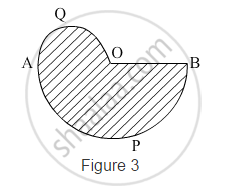
In Fig. 3, APB and AQO are semicircles, and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region [Use `pi=22/7`]
Solution
Let the radius of the semi-circle APB be r
⇒ The radius of the semi-circle AQO =`r/2`
Now,
Perimeter of the given figure = Length of arc AQO + Length of arc APB + OB
`=pixxr/2+pixxr+r`
`=r(3/2pi+1)`
`=r(3/2xx22/7+1)`
`= r((33+7)/7)`
`=r(40/7)cm`
⇒r=7 cm
∴ Area of the shaded region = Area of semi-circle AQO + Area of semi-circle APB
`=(pi(r/2)^2)/2+(pir^2)/2`
`=(pi(7/2)^2)/2+(pixx7^2)/2`
`=(49pi)/8+(49pi)/2`
`=49pi(1/8+1/2)`
`=49xx22/7xx5/8`
= 96.25 cm2
APPEARS IN
RELATED QUESTIONS
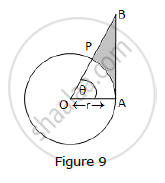
In Fig. 9, is shown a sector OAP of a circle with centre O, containing ∠θ. AB is perpendicular to the radius OQ and meets OP produced at B. Prove that the perimeter of shaded region is
`r[tantheta+sectheta+(pitheta)/180-1]`
A pendulum swings through an angle of 30º and describes an arc 8.8 cm in length. Find the length of the pendulum.
An arc of length 20𝜋 cm subtends an angle of 144° at centre of circle. Find the radius of the circle.
The base of a right – angled triangle measures 48 cm and its hypotenuse measures 50 cm. Find the area of the triangle.
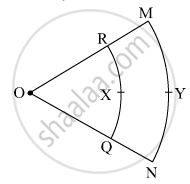
In the given figure, O is the centre of the sector. \[\angle\]ROQ = \[\angle\]MON = 60° . OR = 7 cm, and OM = 21 cm. Find the lengths of arc RXQ and arc MYN. (\[\pi = \frac{22}{7}\])
The radius of a sector of a circle is 7 cm. If the measure of the arc of the sector is 210°, find the area of the sector in case.
In a circle of radius 14 cm, an arc subtends an angle of 120° at the centre. If `sqrt(3) = 1.73` then the area of the segment of the circle is
Draw the circumcircle of Δ PMT in which PM = 5.4, P = 60°, M = 70°.
The perimeter of a square and the circumference of a circle are equal. If the length of each side of the square is 22 cm, find:
(i) perimeter of the square.
(ii) circumference of the circle.
(iii) radius of the circle.
The sum of the circumference and diameter of a circle is 176 cm. Find the area of the circle.
