Advertisements
Advertisements
प्रश्न
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that
Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`
उत्तर
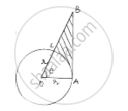
Given angle subtended at centre of circle = 𝜃
∠OAB = 90° [At joint of contact, tangent is perpendicular to radius]
OAB is right angle triangle
Cos 𝜃 =`(adj.side)/(hypotenuse) =r/OB`⇒ 𝑂𝐵 = 𝑟 sec 𝜃 … … (𝑖)
tan 𝜃 =`(opp.side)/(adju.side)=AB/r`⇒ 𝐴𝐵 = 𝑟 tan 𝜃 … … . (𝑖𝑖)
Area of shaded region = (area of triangle) – (area of sector)
`= (1/2× OA × AB) −theta/360^@× pir^2`
`=1/2× r × r tan theta −r^2/2[theta/180^@× pi]`
=`r^2/2[tantheta −(pitheta)/180]`
APPEARS IN
संबंधित प्रश्न
The area of circle, inscribed in equilateral triangle is 154 cms2. Find the perimeter of
triangle.
A square water tank has its side equal to 40m, there are 4 semicircular flower beds grassy plots all around it. Find the cost of turfing the plot at Rs 1.25/sq.m
The length of a chain used as the boundary of a semicircular park is 108 m. Find the area of the park.
The area of a circle inscribed in an equilateral triangle is 154 cm2. Find the perimeter of the triangle.
A horse is tied with a 21 m laig rope to the corner of a field which is in the shape of an equilateral triangle. Find the area of the field over which it can graze.
Find the area and perimeter of the circles with following: Radius = 2.8cm
The circumference of a circle exceeds its diameter by 450 cm. Find the area of the circle.
Find the circumference of the circles whose radii are given below.
49 cm
A circle with radius 16 cm is cut into four equal parts and rearranged to form another shape as shown in the below figure:
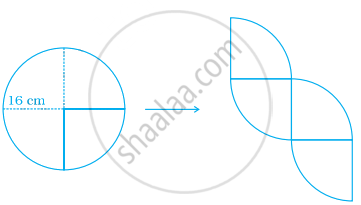
Does the perimeter change? If it does change, by how much does it increase or decrease?
