Advertisements
Advertisements
प्रश्न
The area of a circle inscribed in an equilateral triangle is 154 cm2. Find the perimeter of the triangle.
उत्तर
Let the radius of the inscribed circle be r cm.
Given:
Area of the circle = 154 cm2
We know ;
Area of the circle = πr2
`=> 154 = 22/7"r"^2`
`=> (154xx7)/22 = "r"^2`
⇒ r2 = 49
⇒ r = 7
In a triangle, the centre of the inscribed circle is the point of intersection of the medians and altitudes of the triangle. The centroid divides the median of a triangle in the ratio 2:1.
Here,
AO;OD = 2:1
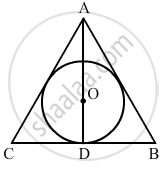
Now,
Let the altitude be h cm
We have :
∠ADB = 90°
OD `=1/3"AD"`
OD `= "h"/3`
⇒ h = 3r
⇒ h = 21
Let each side of the triangle be a cm.
In the right - angled ΔADB, we have ;
AB2 = AD2 + DB2
`"a"^2 = "h"^2 + (a/2)^2`
`4"a"^2 = 4"h"^2 + "a"^2`
`a^2 = 4"h"^2`
`a^2 = (4"h"^2)/3`
`a = (2"h")/sqrt(3)`
`a = 42/sqrt(3) `
∴ Perimeter of the triangle = 3a
`= 3xx42/sqrt(3)`
`= sqrt(3)xx42`
= 72.66 cm
APPEARS IN
संबंधित प्रश्न
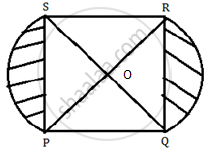
In the figure given below, PQRS is square lawn with side PQ = 42 metres. Two circular flower beds are there on the sides PS and QR with centre at O, the intersections of its
diagonals. Find the total area of the two flower beds (shaded parts).
An arc of a circle is of length 5π cm and the sector it bounds has an area of 20 π cm2. Find the radius of the circle.
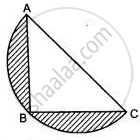
ABC is an isosceles right-angled triangle with ∠ABC = 90°. A semi-circle is drawn with AC as the diameter. If AB = BC = 7 cm, find the area of the shaded region. [Take π = 22/7]
In the given figure, if A(P-ABC) = 154 cm2 radius of the circle is 14 cm, find
(1) `∠APC`
(2) l ( arc ABC) .
In the given figure, OPQR is a rhombus, three of whose vertices lie on a circle with centre O. If the area of the rhombus is `32sqrt(3)`, find the radius of the circle.
The perimeter of a sector of a circle of radius 5.6 cm is 27.2 cm. Find the area of the sector.
Find the area grazed by a horse tied with a 11. 2 m rope to a corner of a field measuring 25m by 15 m.
Find the circumference of the circle whose area is 25times the area of the circle with radius 7cm.
The radius of a circle whose circumference is equal to the sum of the circumferences of the two circles of diameters 36 cm and 20 cm is ______.
Circumference ‘C’ of a circle can be found by multiplying diameter ‘d’ with ______.
