Advertisements
Advertisements
Question
The area of a circle inscribed in an equilateral triangle is 154 cm2. Find the perimeter of the triangle.
Solution
Let the radius of the inscribed circle be r cm.
Given:
Area of the circle = 154 cm2
We know ;
Area of the circle = πr2
`=> 154 = 22/7"r"^2`
`=> (154xx7)/22 = "r"^2`
⇒ r2 = 49
⇒ r = 7
In a triangle, the centre of the inscribed circle is the point of intersection of the medians and altitudes of the triangle. The centroid divides the median of a triangle in the ratio 2:1.
Here,
AO;OD = 2:1
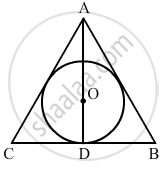
Now,
Let the altitude be h cm
We have :
∠ADB = 90°
OD `=1/3"AD"`
OD `= "h"/3`
⇒ h = 3r
⇒ h = 21
Let each side of the triangle be a cm.
In the right - angled ΔADB, we have ;
AB2 = AD2 + DB2
`"a"^2 = "h"^2 + (a/2)^2`
`4"a"^2 = 4"h"^2 + "a"^2`
`a^2 = 4"h"^2`
`a^2 = (4"h"^2)/3`
`a = (2"h")/sqrt(3)`
`a = 42/sqrt(3) `
∴ Perimeter of the triangle = 3a
`= 3xx42/sqrt(3)`
`= sqrt(3)xx42`
= 72.66 cm
APPEARS IN
RELATED QUESTIONS
Find the circumference of the circle with the following radius: (Take `bb(pi = 22/7`)
14 cm
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find The area of sector
The area of a minor sector of a circle is 3.85 cm2 and the measure of its central angle is 36°. Find the radius of the circle.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. The length of the arc is
Find the area and perimeter of the following sector :
Radius= 6 cm, angle at the centre is 70°
In the given figure, the area of the shaded portion is 770 cm2. If the circumference of the outer circle is 132 cm, find the width of the shaded portion.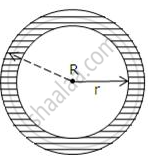
The radius of a circle is 5 m. Find the circumference of the circle whose area is 49 times the area of the given circle.
Complete the table below.
| Radius (r) | Diameter (d) | Circumference (c) |
| ...... | ...... | 72.6 cm |
A bucket is raised from a well by means of a rope wound round a wheel of diameter 35 cm. If the bucket ascends in 2 minutes with a uniform speed of 1.1 m per sec, calculate the number of complete revolutions the wheel makes in raising the bucket.
A photograph of Billiard/Snooker table has dimensions as `1/10`th of its actual size as shown in the given figure:
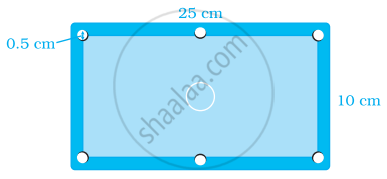
The portion excluding six holes each of diameter 0.5 cm needs to be polished at rate of ₹ 200 per m2. Find the cost of polishing.
