Advertisements
Advertisements
Question
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
Solution
If a square is inscribed in a circle, then the diagonals of the square are diameters of the circle.
Let the diagonal of the square be d cm.
Thus, we have:
Radius , `"r" = "d"/2 "cm"`
Area of the circle = πr2
`= pi"d"^2/4 "cm"^2`
We know ;
`"d"= sqrt(2)xx"Side" `
`=> "Side" = ("d"/sqrt(2)) "cm"`
Area of the the circle = πr2
`=pi"d"^2/4 "cm"^2`
We know ;
`d = sqrt(2)xx"side"`
`⇒ "Side" = "d"/sqrt(2) "cm"`
Area of the square`=("Side")^2`
`=("d"/sqrt(2))^2`
`= "d"^2/2 "cm"^2`
Ratio of the area of the circle to that of the square:
`= (pi"d"^2/4)/("d"^2/2)`
`= pi/2 `
Thus, the ratio of the area of the circle to that of the square is π : 2
APPEARS IN
RELATED QUESTIONS
The adjacent sides of a parallelogram are 32 cm and 24 cm. If the distance between the longer sides is 17.4 cm, find the distance between the shorter sides.
In Figure 5, a circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR =12 cm. Find the lengths of QM, RN and PL ?

In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
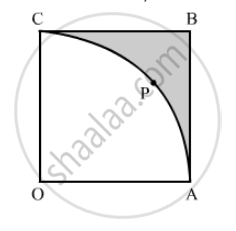
In the following figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. (Use π = 22/7)
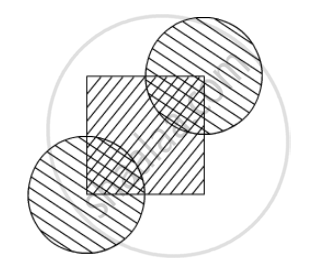
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
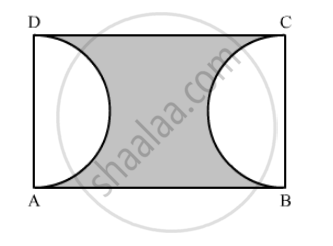
In the given figure, ABCD is a square each of whose sides measures 28 cm. Find the area of the shaded region.

Find the area of a circle of radius 30 cm (use π = 3.14).
Find the length of the rope by which a bull must be tethered in order that it may be able to graze an area of 2464 m2
Lalitha wants to buy a round carpet of radius is 63 cm for her hall. Find the area that will be covered by the carpet
If radius of a circle is increased to twice its original length, how much will the area of the circle increase?
