Advertisements
Advertisements
Question
In Figure 5, a circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR =12 cm. Find the lengths of QM, RN and PL ?

Solution
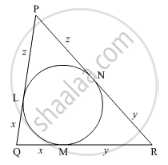
Given: In ΔPQR, PQ = 10, QR = 8 cm and PR = 12 cm.
We know that, the lengths of tangents drawn from an external point to a circle are equal.
∴ QM = OL = x (Say)
RM = RN = y (Say)
PL = PN = z (Say)
QR = QM + MR = x + y = 8 cm ……(1)
PQ = PL + LQ = z + x = 10 cm ……(2)
PR = PN + NR = z + y = 12 cm ……(3)
Adding (1), (2) and (3) , we have
(x + y) + (z + x) + (z + y) = (8 + 10 + 12) = 30 cm
∴ 2(x + y + z) = 30 cm
⇒ x + y + z = 15 cm …..(4)
From (2) and (4), we have
10 + y = 15
∴ y = 5
From (3) and 4, we have
12 + x = 15
∴ x = 3
From (1) and (4), we have
⇒ z + 8 = 15
⇒ z = 7
∴ QM = x = 3 cm
RN = y = 5 cm
PL = z = 7 cm
APPEARS IN
RELATED QUESTIONS
If the numerical value of the area of a circle is equal to the numerical value of its circumference , find its radius.
A wire can be bent in the form of a circle of radius 56 cm. If it is bent in the form fo a square, then its area will be
A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
The areas of two concentric circles are 1386 cm2 and 962.5 cm2. The width of the ring is
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

Find the area enclosed between two concentric circles, If their radii are 6cm and 13cm respectively.
Two circles touch each other externally. The sum of their areas is 58πcm2 and the distance between their centres us 10cm. Find the radii of the two circles.
Diameter of a circular garden is 9.8 m. Find its area.
Is the area of the largest circle that can be drawn inside a rectangle of length a cm and breadth b cm (a > b) is πb2 cm2? Why?
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is ______.
