Advertisements
Advertisements
Question
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

Solution
(i)

Radius of circle, r = 7 cm
∴ Side of square = 7 + 7 = 14 cm
Area of circle = `pir^2`
= `22/7 xx 7xx 7`
= 154 cm2
Area of square = `14 xx 14`
= 196 cm2
∴ Area of shaded portion = 196 - 154
= 42 cm2
(ii)
Radii of concentric circles are
`r_1 = 4.5`m
`r_2 = 2.5`m

∴ Area of shaded portion = `pir_1^2 - pir_2^2`
= `pi[r_1^2 - r_2^2] = 22/7[(4.5)^2 - (2.5)^2]`
= `22/7 xx (4.5 + 2.5) (4.5 - 2.5)`
= `22/7 xx 14 = 44` cm2
APPEARS IN
RELATED QUESTIONS
The cost of fencing a square lawn at ₹ 14 per meter is ₹ 28000. Find the cost of mowing the lawn at ₹ 54 100 per `m^2`
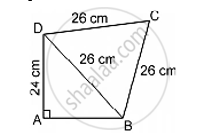
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
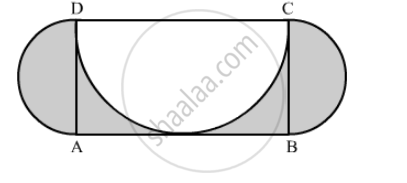
In the following figure, ABCD is a rectangle with AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semi-circles are drawn as shown in the figure. Find the area of the shaded region.
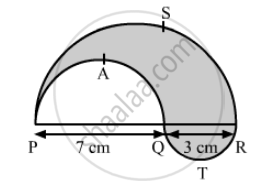
In the the following figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region.
In a hospital used water is collected in a cylindrical tank of diameter 2 m and height 5 m. After recycling, this water is used to irrigate a park of hospital whose length is 25 m and breadth is 20 m. If tank is filled completely then what will be the height of standing water used for irrigating the park.
If the circumference and the area of a circle are numerically equal, then diameter of the circle is
The area of a circle is 220 cm2. The area of ta square inscribed in it is
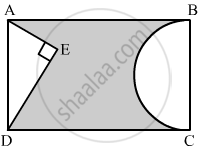
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
The areas of two concentric circles are 1386 cm2 and 962.5 cm2. The width of the ring is
The diameters of three circles are in the ratio 3: 5: 6. If the sum of the circumferences of these circles is 308 cm; find the difference between the areas of the largest and the smallest of these circles.
