Advertisements
Advertisements
Question
The radii of the inner and outer circumferences of a circular running track are 63 m and 70 m respectively. Find :
(i) the area of the track ;
(ii) the difference between the lengths of the two circumferences of the track.
Solution

Outer radius, r1 = 70 m
Inner radius, r2 = 63 m
∴ Area of track = `pir_1^2 - pir_2^2`
= `22/7[(70)^2 - (63)^2]`
= `22/7(70 + 63)(70 - 63)`
= `22/7 xx 133 xx 7`
= 2926 m2
Length of outer edge i.e. circumference
= `2pir_1`
= `2 xx 22/7 xx 70 = 440`m
Length of inner edge = `2pir_2`
= `2 xx 22/7 xx 63 = 396` m
Difference between lengths of two circumferences = 440 – 396 = 44 m
Hence (i) 2926 m2 (ii) 44 m
APPEARS IN
RELATED QUESTIONS
Find the area of the following circle, given that diameter = 49 m.
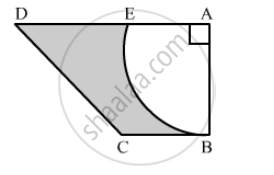
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
Write the formula for the area of a segment in a circle of radius r given that the sector angle is \[\theta\] (in degrees).
Find the area of sector of circle of radius 21 cm and central angle 1200.
A wire can be bent in the form of a circle of radius 56 cm. If it is bent in the form fo a square, then its area will be
If the area of the circle is numerically equal to twice its circumference then what is the diameter of the circle?
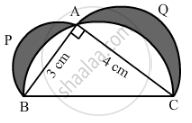
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
Find the area of the dining table whose diameter is 105 cm
The area of the circle whose diameter is 21 cm is ____________.
