Advertisements
Advertisements
Question
Find the area of sector of circle of radius 21 cm and central angle 1200.
Solution
Area of a sector of a circle = \[\frac{\theta}{360} \times \pi r^2\]
\[= \frac{120}{360} \times \pi \left( 21 \right)^2 \]
\[ = 462 {cm}^2\]
APPEARS IN
RELATED QUESTIONS
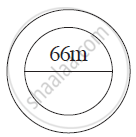
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
The perimeter of a rectangular plot of land is 80 m and its breadth is 16 m. Find the length and area of the plot.
The cost of painting the four walls of a room 12 m long at `₹ 30 per m^2 is ₹ 7560 per m^2` and the cost of covering the floor with the mat at ₹` 25 per m^2 is ₹ 2700 `. find the dimensions of the room.
The cost of fencing a square lawn at ₹ 14 per meter is ₹ 28000. Find the cost of mowing the lawn at ₹ 54 100 per `m^2`
If the circumference of a circle increases from 4π to 8π, then its area is
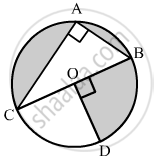
In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of shaded region.
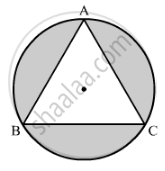
On a circular table cover of radius 42 cm, a design is formed by a girl leaving an equilateral triangle ABC in the middle, as shown in the figure. Find the covered area of the design. `["Use" sqrt(3) = 1.73, pi =22/7]`
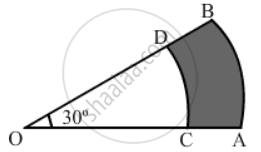
In the given figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.
The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km per hour.
The diameters of three circles are in the ratio 3: 5: 6. If the sum of the circumferences of these circles is 308 cm; find the difference between the areas of the largest and the smallest of these circles.
