Advertisements
Advertisements
Question
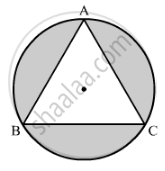
On a circular table cover of radius 42 cm, a design is formed by a girl leaving an equilateral triangle ABC in the middle, as shown in the figure. Find the covered area of the design. `["Use" sqrt(3) = 1.73, pi =22/7]`
Solution
Construction: Join AO and extend it to D on BC.
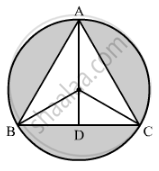
Radius of the circle, r = 42 cm
∠OCD= 30°
cos30° `= "DC"/"OC"`
`=> sqrt(3)/2 = "DC"/42`
`⇒ "DC" = 21sqrt(3)`
`=> "DC" = 2xx"DC" = 42sqrt(3) = 72.66 "cm"`
sin 30°`="OD"/"OC"`
`=> 1/2="OD"/42`
⇒ OD = 21 cm
Now, AD = AO + OD = 42 + 21 = 63 cm
Area of shaded region = Area of circlec - Area of triangle ABC
`= pi(OA)^2-1/2xx"AD"xx"AB"`
`=22/7(42)^2-1/2xx63xx72.66`
= 5544 - 2288.79
= 3255.21 cm2
APPEARS IN
RELATED QUESTIONS
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the length of the arc. (Use π = `22/7`)
Write the formula for the area of a segment in a circle of radius r given that the sector angle is \[\theta\] (in degrees).
If the circumference and the area of a circle are numerically equal, then diameter of the circle is
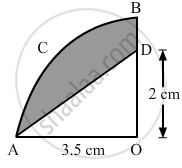
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
The radius of a wheel is 0.25 m. How many revolutions will it make in covering 11 km?
In the given figure, ABCD is a square each of whose sides measures 28 cm. Find the area of the shaded region.

Find the area of the biggest circle that can be cut from a rectangular piece 44cm by 28cm. also, find the area of the paper left after cutting out the circle.
If the perimeter of a semicircular protractor is 72 cm where `pi = 22/7`, then the diameter of protractor is ____________.
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is ______.
