Advertisements
Advertisements
Question
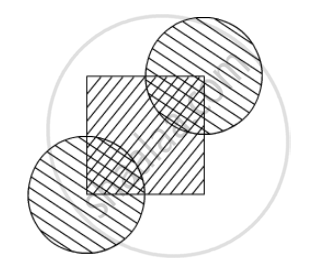
In the given figure, ABCD is a square each of whose sides measures 28 cm. Find the area of the shaded region.

Solution
Let r be the radius of the circle.
Thus, we have:
`r = 28/2 "cm"`
= 14 cm
Now,
Area of the shaded region =(Arae of the square ABCD) - 4(Area of the sector where r = 14 cm and θ = 90°)
`=|(28xx28)-4(22/7xx14xx14xx90/360)|"cm"^2`
`=|784 - 4(154)| "cm"^2`
= (784 - 616) cm2
= 168 cm2
APPEARS IN
RELATED QUESTIONS
From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed. (as shown in the following figure). Find the area of the remaining sheet. (Take `pi = 22/7`)

The area of rectangle is `192cm^2` and its perimeter is 56 cm. Find the dimensions of the rectangle.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
The area of the incircle of an equilateral triangle of side 42 cm is
If the area of a sector of a circle is `5/18` of the area of the circle, then the sector angle is equal to
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
The diameter of a wheel is 40 cm. How many revolutions will it make in covering 176 m?
Find the length of the rope by which a bull must be tethered in order that it may be able to graze an area of 2464 m2
If radius of a circle is increased to twice its original length, how much will the area of the circle increase?
