Advertisements
Advertisements
Question
From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed. (as shown in the following figure). Find the area of the remaining sheet. (Take `pi = 22/7`)

Solution
Area of bigger circle = `22/7 xx 14 xx 14`
= 616 cm2
Area of 2 small circles = `2 xx pir^2`
= `2 xx 22/7 xx 3.5 xx 3.5`
= 77 cm2
Area of rectangle = Length × Breadth
= 3 × 1
= 3 cm2
Remaining area of sheet = 616 - 77 - 3
= 536 cm2
APPEARS IN
RELATED QUESTIONS
The area of a square filed is 8 hectares. How long would a man take to cross it diagonally by walking at the rate of 4 km per hour?
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
In the following figure, AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.

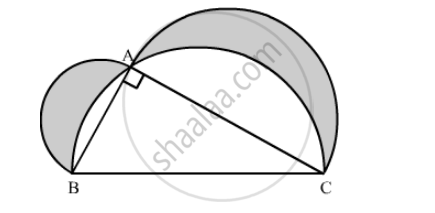
In the following figure, ABC is a right angled triangle in which ∠A = 90°, AB = 21 cm and AC = 28 cm. Semi-circles are described on AB, BC and AC as diameters. Find the area of the shaded region.
The area of the largest triangle that can be inscribed in a semi-circle of radius r, is
The area of a circle is 220 cm2. The area of ta square inscribed in it is
If diameter of a circle is increased by 40%, then its area increase by
Find the area enclosed between two concentric circles, If their radii are 6cm and 13cm respectively.
Find the area of the dining table whose diameter is 105 cm
Perimeter of a sector of a circle whose central angle is 90° and radius 7 cm is ____________.
