Advertisements
Advertisements
Question
The area of a circle is 220 cm2. The area of ta square inscribed in it is
Options
49 cm2
70 cm2
140 cm2
150 cm2
Solution
∴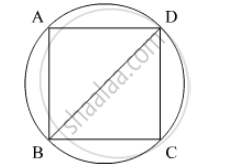
Let BD be the diameter and diagonal of the circle and the square respectively.
We know that area of the circle `=pir^2`
Area of the circle =`pir^2`
`∴ 220=22/7xxr^2`
Multiplying both sides of the equation by 7 we get,
`220xx7=22xxr^2`
Dividing both sides of the equation by 22 we get,
`∴ r^2=70`
`∴r=sqrt70`
As we know that diagonal of the square is the diameter of the square.
`∴ "Diagonal"=2r`
`∴ "Diagonal"=2sqrt70`
`∴ "side of the square"= "diagonal"/sqrt2` ................(1)
Substituting Diagonal=`2sqrt70` in equation (1) we get,
side of the square=`(2sqrt70)/2`
∴ side of the square= `2sqrt(70/2)`
∴ side of the square=`2sqrt35`
∴ Area of the square=`"side "^2`
=`(2sqrt35)^2`
=`4xx35`
= `140`
Therefore, area of the square is.`140 cm^2`
APPEARS IN
RELATED QUESTIONS
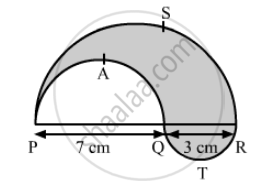
In the the following figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region.
If the circumference and the area of a circle are numerically equal, then diameter of the circle is
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then the radius of the circle
A pendulum swings through an angle of 30° and describes an arc 8.8 cm in length. Find the length of the pendulum.
The given figures show a rectangle ABCD inscribed in a circle as shown alongside.
If AB = 28 cm and BC = 21 cm, find the area of the shaded portion of the given figure.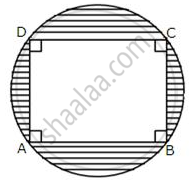
Find the radius and circumference of a circle, whose area is :
(i) 154 cm2
(ii) 6.16 m2
A lawn is in the shape of a semicircle of diameter 42m. the lawn is surrounded by a flower bed of width 7m all round. Find the area of the flower bed in m2.
Area of circle of radius ‘n’ units is
The area of the circle whose diameter is 21 cm is ____________.
Area of the circle obtained in 196 m2 is ______.
