Advertisements
Advertisements
Question
In the following figure, ABC is a right angled triangle in which ∠A = 90°, AB = 21 cm and AC = 28 cm. Semi-circles are described on AB, BC and AC as diameters. Find the area of the shaded region.
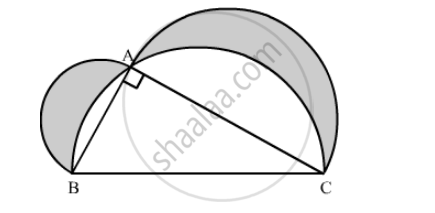
Solution
We have given three semi-circles and one right angled triangle.
`"∴ Area ofshaded region=Area of semi-circle with AB as a diameter"`
`"+ Area of semi-circle with AC as a diameter"`
`"+ Area of right angled ABC"`
` "-Area of semi-circle with BC as a diameter"`
Let us calculate the area of the semi-circle with AB as a diameter.
`∴"Area of semi-circle with AB as a diameter"=(pir^2)/2`
`∴ "Area of semi-circle with AB as a diameter"=pi/2(21/2)^2`
` "Area of semi-circle with AB as a diameter"=pi/2(21/2)^2`
Now we will find the area of the semi-circle with AC as a diameter.
`"Area of semi-circle with AC as a diameter"=pir^2/2`
`"Area of semi-circle with AC as a diameter"pi(28/2)^2/2`
`"Area of semi-circle with AC as a diameter"pi/2(28/2)^2`
Now we will find the length of BC.
In right angled triangle ABC, we will use Pythagoras theorem,
`BC^2=AB^2+AC^2`
`∴ BC^2=21^2+28^2`
`∴BC^2=441+784`
`∴BC^2=1225`
`∴ BC=35`
Now we will calculate the area of the right angled triangle ABC.
`A(ΔABC)=1/2xxABxxAC`
`∴ A(ΔABC)=1/2xx21xx28`
`∴A(ΔABC)=21xx14`
`∴ A(ΔABC)=294`
Now we will find the area of the semi-circle with BC as a diameter.
`"Area of semi-circle with BC as a diameter"=`(pi r^2)/2`
`∴" Area of semi-circle with AB as a diameter"=pi(35/2)^2/2`
`∴ " Area of semi-circle with AB as a diameter"=pi/2(35/2)^2`
Now we will substitute all these values in equation (1).
`∴ "Area of the shaded region"=pi/2(21/2)^2+pi/2(28/2)^2+294-pi/2(35/2)^2`
`∴ "Area of the shaded region"=pi/8(21^2+28^2-35^2)+294`
`∴ "Area of the shaded region"=pi/8(441+784-1225)+294`
`∴"Area of the shaded region"pi/8(1225-1225)+294`
`∴"Area of the shaded region"=294`
Therefore, area of shaded region is `294 cm^2`
APPEARS IN
RELATED QUESTIONS
Find the area of the following circles, given that radius = 5 cm.
Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle , such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles . Find the radius of the third circle correct to one decimal place.
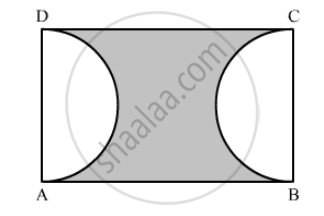
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the length of the boundary of the shaded region.
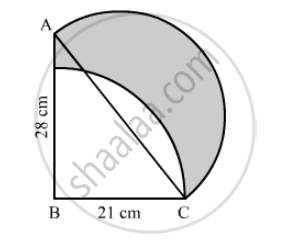
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
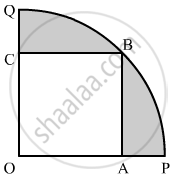
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
The radius of a wheel is 0.25 m. How many revolutions will it make in covering 11 km?
The diameters of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to the sum of the areas of the two given circles.
The area of the circle that can be inscribed in a square of side 6 cm is ______.
