Advertisements
Advertisements
प्रश्न
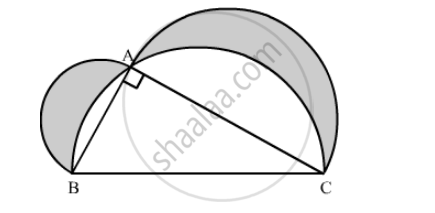
In the following figure, ABC is a right angled triangle in which ∠A = 90°, AB = 21 cm and AC = 28 cm. Semi-circles are described on AB, BC and AC as diameters. Find the area of the shaded region.
उत्तर
We have given three semi-circles and one right angled triangle.
`"∴ Area ofshaded region=Area of semi-circle with AB as a diameter"`
`"+ Area of semi-circle with AC as a diameter"`
`"+ Area of right angled ABC"`
` "-Area of semi-circle with BC as a diameter"`
Let us calculate the area of the semi-circle with AB as a diameter.
`∴"Area of semi-circle with AB as a diameter"=(pir^2)/2`
`∴ "Area of semi-circle with AB as a diameter"=pi/2(21/2)^2`
` "Area of semi-circle with AB as a diameter"=pi/2(21/2)^2`
Now we will find the area of the semi-circle with AC as a diameter.
`"Area of semi-circle with AC as a diameter"=pir^2/2`
`"Area of semi-circle with AC as a diameter"pi(28/2)^2/2`
`"Area of semi-circle with AC as a diameter"pi/2(28/2)^2`
Now we will find the length of BC.
In right angled triangle ABC, we will use Pythagoras theorem,
`BC^2=AB^2+AC^2`
`∴ BC^2=21^2+28^2`
`∴BC^2=441+784`
`∴BC^2=1225`
`∴ BC=35`
Now we will calculate the area of the right angled triangle ABC.
`A(ΔABC)=1/2xxABxxAC`
`∴ A(ΔABC)=1/2xx21xx28`
`∴A(ΔABC)=21xx14`
`∴ A(ΔABC)=294`
Now we will find the area of the semi-circle with BC as a diameter.
`"Area of semi-circle with BC as a diameter"=`(pi r^2)/2`
`∴" Area of semi-circle with AB as a diameter"=pi(35/2)^2/2`
`∴ " Area of semi-circle with AB as a diameter"=pi/2(35/2)^2`
Now we will substitute all these values in equation (1).
`∴ "Area of the shaded region"=pi/2(21/2)^2+pi/2(28/2)^2+294-pi/2(35/2)^2`
`∴ "Area of the shaded region"=pi/8(21^2+28^2-35^2)+294`
`∴ "Area of the shaded region"=pi/8(441+784-1225)+294`
`∴"Area of the shaded region"pi/8(1225-1225)+294`
`∴"Area of the shaded region"=294`
Therefore, area of shaded region is `294 cm^2`
APPEARS IN
संबंधित प्रश्न
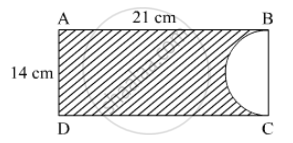
In the given figure, ABCD is rectangle of dimensions 21 cm × 14 cm. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure.
Find the area of a parallelogram with base equal to 25 cm and the corresponding height measuring 16.8 cm.
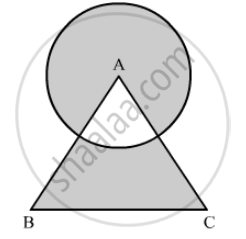
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then the radius of the circle
In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region. [Use π= 3.14]

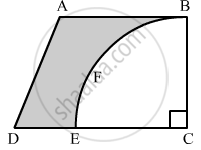
From a thin metallic piece in the shape of a trapezium ABCD in which AB || CD and ∠BCD = 90°, a quarter circle BFEC is removed. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of remaining (shaded) part of metal sheet.
A square is inscribed in a circle of radius 7 cm. Find the area of the square.
A square is inscribed in a circle of radius 6 cm. Find the area of the square. Give your answer correct to two decimal places if `sqrt(2)` = 1.414.
If the radius of a circle is doubled, its area becomes ____________.
